Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(x^2=y.z\Rightarrow\frac{x}{y}=\frac{z}{x}\)
tuong tự ta có\(\frac{x}{y}=\frac{z}{x}=\frac{y}{z}=\frac{x+z+y}{y+x+z}=1\)
=> dpcm
Lile nhá bạn
a.
\(x^2+\left(y+z\right)x+yz=x^2+xy+xz+yz=\left(x+y\right)x+\left(x+y\right)z=\left(x+y\right)\left(x+z\right)\)
b.
\(\left(x-y\right)^3=x^3-3x^{2y}+3xy^2-y^3\) (lập phương của một hiệu)
\(\Rightarrow x^3-y^3=\left(x-y\right)^3+3x^2y-3xy^2=\left(x-y\right)^3+3xy\left(x-y\right)=\left(x-y\right)\left[\left(x-y\right)^2+3xy\right]=\left(x-y\right)\left(x^2-2xy+y^2+3xy\right)=\left(x-y\right)\left(x^2+xy+y^2\right)\)
Chúc bạn học tốt ^^
a.
\(x^2+\left(y+z\right)x+yz=x^2+xy+xz+yz=x\left(x+y\right)+z\left(x+y\right)=\left(x+y\right)\left(x+z\right)\)
b.
\(\left(x-y\right)^3=x^3-3x^2y+3xy^2-y^3\)(lập phương của một hiệu)
\(\Rightarrow x^3-y^3=\left(x-y\right)^3+3x^2y-3xy^2=\left(x-y\right)^3+3xy\left(x-y\right)=\left(x-y\right)\left[\left(x-y\right)^2+3xy\right]=\left(x-y\right)\left(x^2-2xy+y^2+3xy\right)=\left(x-y\right)\left(x^2+xy+y^2\right)\)
Chúc bạn học tốt ^^
\(Gt\Rightarrow x^2+y^2+z^2=xy+yz+zx\)
\(\Leftrightarrow2x^2+2y^2+2z^2-2xz-2yz-2zx=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2=0\)
Do VT > 0 nên dấu "=" <=> x = y = z (DpcM)
a/ \(C=\left(x^3+x^2y-2x^2\right)-\left(xy+y^2-2y\right)+\left(x+y-1\right)\)
\(C=x^2\left(x+y-2\right)-y\left(x+y-2\right)+\left(x+y-1\right)=x+y-1\) (do x+y-2=0)
Mà x+y-2=0 => x+y-1=1 => C=1
b/ Với x=2; y=2 Ta nhận thấy \(x^3-2y^2=2^3-2.2^2=2^3-2^3=0\) => D=0
A + B + C = x2.y.z + x.y2.z + x.y.z2 = x.y.z.(x + y + z) = x.y.z .1 = xyz (Vì x+ y + z = 1)
Theo đề bài ta có:
cân bằng phương trình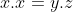
bằng cách nhân x vào cả hai vế ta có:
cân bằng phương trình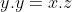
bằng cách nhân y vào cả hai vế ta có:
cân bằng phương trình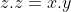
bằng cách nhân z vào cả hai vế ta có:
vì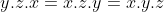
Vì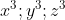
Có cùng số mũ và bằng nhau
Nên các cơ số cũng bằng nhau
Ta có: \(x^2=y\cdot z\)
nên \(z=\dfrac{x^2}{y}\)(1)
Ta có: \(y^2=z\cdot x\)
nên \(z=\dfrac{y^2}{x}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x^2}{y}=\dfrac{y^2}{x}\)
\(\Leftrightarrow x^3=y^3\)
hay x=y(3)
Ta có: \(x^2=y\cdot z\)
nên \(y=\dfrac{x^2}{z}\)(4)
Ta có: \(z^2=x\cdot y\)
nên \(y=\dfrac{z^2}{x}\)(5)
Từ (4) và (5) suy ra \(\dfrac{x^2}{z}=\dfrac{z^2}{x}\)
\(\Leftrightarrow x^3=z^3\)
hay x=z(6)
Từ (3) và (6) suy ra x=y=z(đpcm)