Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
$A=2+2^2+2^3+2^4+...+2^{10}$
$=(2+2^2+2^3+2^4)+(2^5+2^6+2^7+2^8)+2^9+2^{10}$
$=2(1+2+2^2+2^3)+2^5(1+2+2^2+2^3)+2^9(1+2)$
$=15(2+2^5)+3.2^9$
Ta thấy $15(2+2^5)\vdots 5$ còn $3.2^9\not\vdots 5$
$\Rightarrow A\not\vdots 5$
Bài 2:
$B=2+2^2+2^3+2^4+...+2^{99}+2^{100}$
$=(2+2^2)+(2^3+2^4)+(2^5+2^6)+...+(2^{99}+2^{100})$
$=2(1+2)+2^3(1+2)+2^5(1+2)+...+2^{99}(1+2)$
$=(1+2)(2+2^3+2^5+...+2^{99})$
$=3(2+2^3+2^5+...+2^{99})\vdots 3$

3.
\(C=5+5^2+...+5^6\\ C=5\left(1+5\right)+5^3\left(1+5\right)+5^5\left(1+5\right)\\ C=5\cdot6+5^3\cdot6+5^5\cdot6\\ C=6\left(5+5^3+5^5\right)\\ =>C⋮6\)
\(4.D=3+3^2+...+3^6\\D=3\left(1+3\right)+3^3\left(1+3\right)+3^5\left(1+3\right)\\ D=3\cdot4+3^3\cdot4+3^5\cdot5\\ C=4\left(3+3^3+3^5\right)\\ =>D⋮4\\ 5.E=4+4^2+...+4^6\\ E=4\left(1+4\right)+4^3\left(1+4\right)+4^5\left(1+4\right)\\ E=4\cdot5+4^3\cdot5+4^5\cdot5\\ E=5\left(4+4^3+4^5\right)=>E⋮5 \)

Vì `|x+2|+|x+2/5|+|x+1/2|>=0`
`=>4x>=0`
`=>x>=0`
`=>|x+2|=x+2,|x+2/5|=x+2/5,|x+1/2|=x+1/2`
`=>x+2+x+2/5+x+1/2=4x`
`=>3x+5/2+2/5=4x`
`=>4x-3x=5/2+2/5=29/10`
`=>x=29/10(tmđk)`
Vậy `x=29/10`
Giải:
Vì \(\left|x+2\right|+\left|x+\dfrac{2}{5}\right|+\left|x+\dfrac{1}{2}\right|\ge0\) nên ta có:
\(\left|x+2\right|+\left|x+\dfrac{2}{5}\right|+\left|x+\dfrac{1}{2}\right|=4x\)
\(\left(x+2\right)+\left(x+\dfrac{2}{5}\right)+\left(x+\dfrac{1}{2}\right)=4x\)
\(x+2+x+\dfrac{2}{5}+x+\dfrac{1}{2}=4x\)
\(\left(x+x+x\right)+\left(2+\dfrac{2}{5}+\dfrac{1}{2}\right)=4x\)
\(3x+\dfrac{29}{10}=4x\)
\(3x-4x=-\dfrac{29}{10}\)
\(-1x=-\dfrac{29}{10}\)
\(x=-\dfrac{29}{10}:-1\)
\(x=\dfrac{29}{10}\)


pạn nào giải giúp mình bài này trước 16h đc ko ( mình năn nỉ đó )![]()

\(\left(2x-1\right)^5+243=0\)
=>\(\left(2x-1\right)^5=-243\)
=>\(\left(2x-1\right)^5=\left(-3\right)^5\)
=>2x-1=-3
=>2x=-2
=>\(x=-\dfrac{2}{2}=-1\)
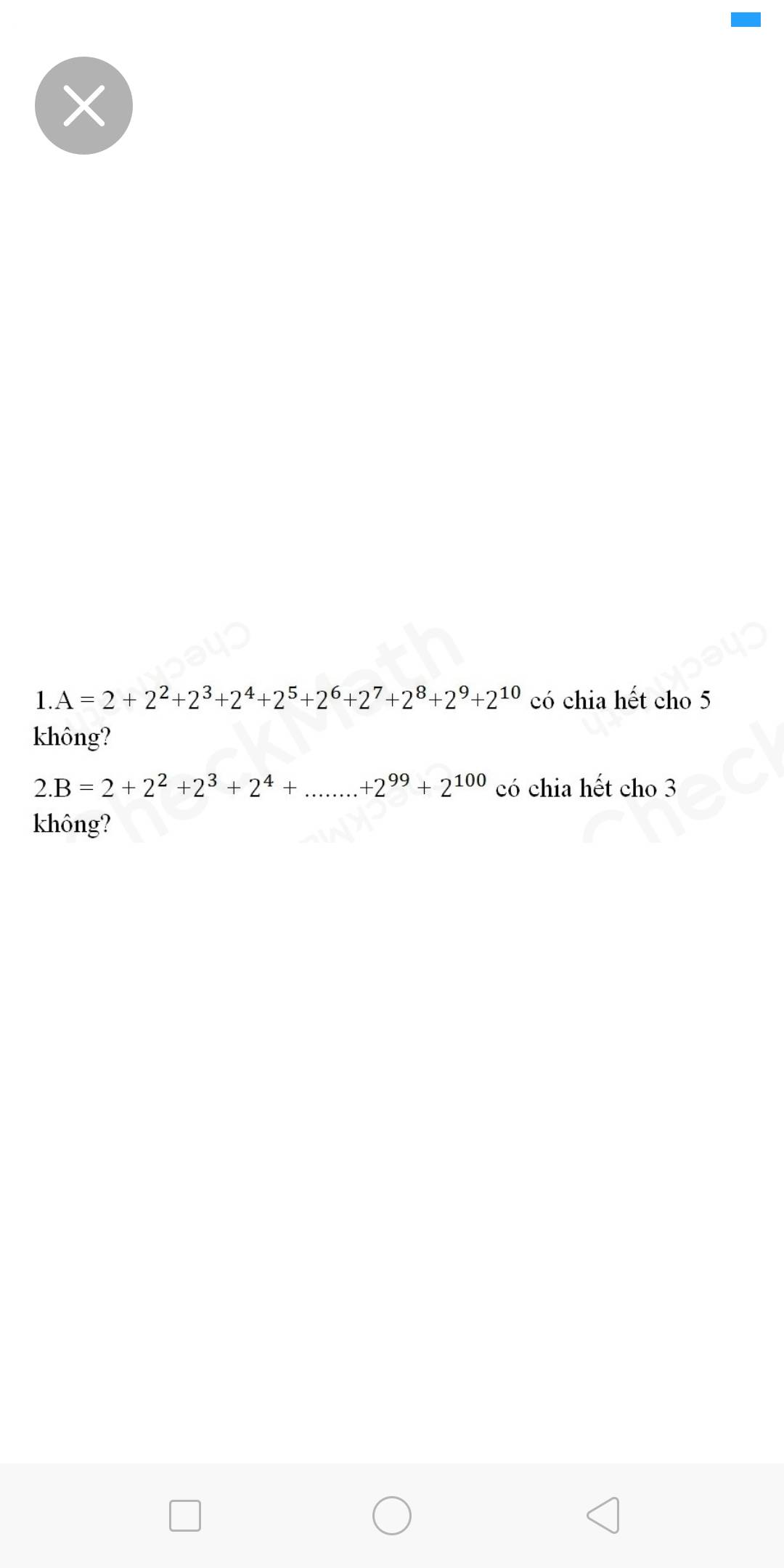



 Mik đng cần gấp giải đc bài nào thì ha bài ấy nha!!!!C.ơn trc nha.
Mik đng cần gấp giải đc bài nào thì ha bài ấy nha!!!!C.ơn trc nha.
\(4x^3=4x\)
=>\(x^3=x\)
=>\(x^3-x=0\)
=>\(x\cdot\left(x^2-1\right)=0\)
=>\(x\left(x-1\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x-1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=1\\x=-1\end{matrix}\right.\)
4x³ = 4x
4x³ - 4x = 0
4x(x² - 1) = 0
4x = 0 hoặc x² - 1 = 0
*) 4x = 0
x = 0
*) x² - 1 = 0
x² = 1
x = 1 hoặc x = -1
Vậy x = -1; x = 0; x = 1