Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

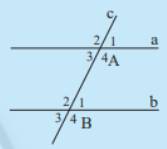
a) Ta có: \(\widehat {{B_2}}\) và \(\widehat {{A_1}}\) là hai góc ở vị trí so le trong. Đo góc ta được: \(\widehat {{B_2}}\)= \(\widehat {{A_1}}\)
b) Ta có: \(\widehat {{B_1}}\) và \(\widehat {{A_1}}\) là hai góc ở vị trí đồng vị. Đo góc ta được: \(\widehat {{B_1}}\)= \(\widehat {{A_1}}\)

Nếu một đường thẳng cắt hai đường thẳng song song thì theo tính chất của hai đường thẳng song song ta có:
+) Mỗi cặp góc so le trong bằng nhau.
+) Mỗi cặp góc đồng vị bằng nhau.
+) Mỗi cặp góc trong cùng phía bù nhau.
Do đó, các kết quả trên đều đúng

ta giả sử rằng hai đường thẳng a và b là không song song với nhau :
khi đó a phải cắt b, ta gọi giao điểm của chúng là điểm O

Ta có \(\hept{\begin{cases}A_1=B_1\\B_1+B_2=180^0\end{cases}\Rightarrow A_1+B_2=180^0}\)
mà xét trong tam giác ABO có : \(A_1+B_2+O=180^0\Rightarrow O=0^0\) điều này là vô lý
vậy giả sử sai hay a phải song song với b

a) Ta có hình vẽ:
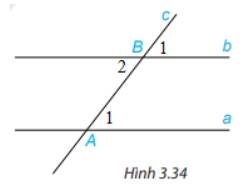
a) Cặp góc đồng vị có số đo = 130o là aAc và bBc
b) Cặp góc so le trong có số đo = 50o là aAB và ABb'
c) Cặp góc trong cùng phía là: aAB và ABb, tổng số đo 2 góc này = 180o vì 2 góc đồng vị = nhau nên 2 đường thẳng aa' và bb' song song => 2 cặp góc trong cùng phía bù nhau