Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi : c là nhiệt dung riêng của nước ; m là khối lượng nước chứa trong một ca ;
n1 và n2 lần lượt là số ca nước múc ở thùng A và thùng B ;
(n1 + n2) là số ca nước có sẵn trong thùng C.
- Nhiệt lượng do n1 ca nước ở thùng A khi đổ vào thùng C đã hấp thụ là :
Q1 = n1.m.c(50 – 20) = 30cmn1
- Nhiệt lượng do n2 ca nước ở thùng B khi đổ vào thùng C đã toả ra là :
Q2 = n2.m.c(80 – 50) = 30cmn2
- Nhiệt lượng do (n1 + n2) ca nước ở thùng C đã hấp thụ là :
Q3 = (n1 + n2)m.c(50 – 40) = 10cm(n1 + n2)
- Phương trình cân bằn nhiệt : Q1 + Q3 = Q2
Þ 30cmn1 + 10cm(n1 + n2) = 30cmn2 Þ 2n1 = n2
Vậy, khi múc n ca nước ở thùng A thì phải múc 2n ca nước ở thùng B và số nước đã có sẵn trong thùng C trước khi đổ thêm là 3n ca.

Giả sử thùng có khối lượng mt, nhiệt dung riêng ct
PT cân bằng nhiệt ban đầu: \(m_t.c_t.(70-25)+m.c.(70-25)=2m.c.(100-70)\)
\(\Rightarrow m_t.c_t.45 = m.c.15\Rightarrow 3m_t.c_t=m.c\)
Khi đổ hết nước trong thùng, gọi nhiệt độ cân bằng là t, ta có:
\( m_t.c_t(t-25)=2m.c.(100-t)\)
\(\Rightarrow m_t.c_t(t-25)=2.3m_t.c_t.(100-t)\)
\(\Rightarrow t-25=6(100-t)\)
\(\Rightarrow t = 89,3^0C\)

Ở trường hợp đầu
Sau khi cân bằng nhiệt
\(Q_{tỏa}=Q_{thu}\Rightarrow m_nc_n\cdot\left(t_đ-t_s\right)=m_{thùng}c_{thùng}\cdot\left(t_s-t_đ'\right)+m_nc_n\left(t_s-t_đ''\right)\)
\(\Rightarrow m_nc_n\left(100-40-40+20\right)=m_{thùng}c_{thùng}\left(40-20\right)\)
\(\Leftrightarrow2m_nc_n=m_{thùng}c_{thùng}\)
Trường hợp 2
Sau khi cân bằng
\(Q_{tỏa}=Q_{thu}\Rightarrow m_nc_n\cdot\left(t_đ-t_s'\right)=m_{thùng}c_{thùng}\cdot\left(t_s'-t_đ'\right)\)
\(m_nc_n\left(100-t_s'\right)=2m_nc_n\left(t'_s-20\right)\Rightarrow\left(100-t_s'\right)=2\left(t'_s-20\right)\Rightarrow t'_s=\dfrac{140}{3}\left(^oC\right)\)

Đổi: \(500g=0,5kg,50g=0,05kg\)
Nhiệt lượng nước thu vào để đạt đến \(55^0C\) là :
\(Q_{thu}=m_n.c_n.\Delta t=94500\left(J\right)\)
Giả sử ta đổ cùng một lúc một khối nước có khối lượng gồm n cốc vào bình.
\(\Rightarrow\) Khối lượng khối nước đó là : \(m=n.0,05\)
\(\Rightarrow\)Nhiệt lượng mà khối nước tỏa ra là: \(Q=m.c_n.\Delta t=n.0,05.4200.5=1050.n\left(J\right)\)
\(\Rightarrow1050.n=94500\)
\(\Rightarrow n=90\)
Vậy ta cần đổ - múc tối thiểu 90 lượt thì sẽ được nước có yêu cầu như đề bài!!
Đâu phải nhiệt toả ra của mỗi cốc nước nước luôn bằng nhau trong mỗi lượt đâu mà bạn chia

- Gọi : c là nhiệt dung riêng của nước ; m là khối lượng nước chứa trong một ca ;
n1 và n2 lần lượt là số ca nước múc ở thùng A và thùng B ;
(n1 + n2) là số ca nước có sẵn trong thùng C.
- Nhiệt lượng do n1 ca nước ở thùng A khi đổ vào thùng C đã hấp thụ là :
Q1 = n1.m.c(50 – 20) = 30cmn1
- Nhiệt lượng do n2 ca nước ở thùng B khi đổ vào thùng C đã toả ra là :
Q2 = n2.m.c(80 – 50) = 30cmn2
- Nhiệt lượng do (n1 + n2) ca nước ở thùng C đã hấp thụ là :
Q3 = (n1 + n2)m.c(50 – 40) = 10cm(n1 + n2)
- Phương trình cân bằn nhiệt : Q1 + Q3 = Q2
=> 30cmn1 + 10cm(n1 + n2) = 30cmn2 => 2n1 = n2
- Vậy, khi múc n ca nước ở thùng A thì phải múc 2n ca nước ở thùng B và số nước đã có sẵn trong thùng C trước khi đổ thêm là 3n ca.
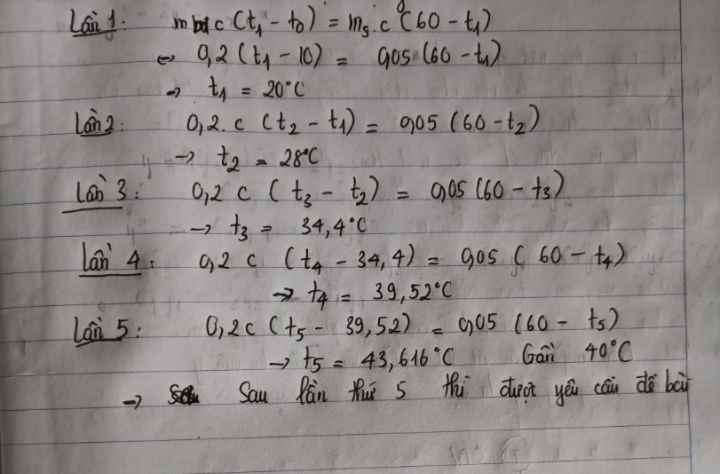
gọi m là khối lượng nước múc từ ca
na,nb lần lượt là ca múc từ thùng A và thùng B
ta có phương trình cân bằng nhiệt:
QA=QB+QC
\(\Leftrightarrow m_AC\left(t_A-t\right)=m_BC\left(t-t_B\right)+m_CC\left(t-t_C\right)\)
\(\Leftrightarrow n_Am\left(t_A-t\right)=n_Bm\left(t-t_B\right)+\left(n_A+n_B\right)m\left(t-t_C\right)\)
\(\Leftrightarrow n_A\left(80-50\right)=n_B\left(50-30\right)+\left(n_A+n_B\right)\left(50-40\right)\)
\(\Leftrightarrow30n_A=30n_B+10n_A+10n_B\)
\(\Leftrightarrow20n_A=40n_B\)
\(\Rightarrow n_A=2n_B\)
vậy số ca múc ở thùng B gấp hai lần số ca múc ở thùng A
câu trả lời quá đúng
anh cho 10 điểm