Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

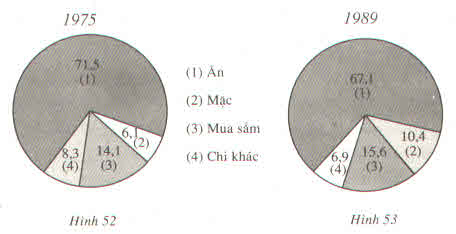
Cơ cấu chi tiêu của người dân Việt Nam, phân theo các khoản chi
| Các khoản chi | Số phần trăm | |
| 1975 | 1989 | |
| Ăn | 71,5 | 67,1 |
| Mặc | 6,1 | 10,4 |
| Mua sắm | 14,1 | 15,6 |
| Chi khác | 8,3 | 6,9 |
| Cộng | 100 (%) | 100 (%) |

Dễ thấy:
\(AD = BC\) nhưng \(AD\) và \(BC\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) không bằng nhau.
\(CD > AB\) do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không bằng nhau.
\(AC\) và \(BD\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) không bằng nhau.

Tham khảo:
Kí hiệu O, E, F là các điểm như trên hình vẽ.
Dễ thấy: tứ giác OEMF là hình bình hành nên \(\overrightarrow {OE} + \overrightarrow {OF} = \overrightarrow {OM} \) hay \(\overrightarrow v + \overrightarrow u = \overrightarrow {OM} \)
Và \(\overrightarrow {OC} = 3.\overrightarrow {OM} \Rightarrow 3\left( {\overrightarrow v + \overrightarrow u } \right) = 3.\overrightarrow {OM} = \overrightarrow {OC} \)
Mặt khác: \(\overrightarrow {OA} = 3.\overrightarrow {OF} = 3\;\overrightarrow u ;\;\overrightarrow {OB} = 3.\overrightarrow {OE} = 3\;\overrightarrow v \)
Và \(\overrightarrow {OB} + \overrightarrow {OA} = \overrightarrow {OC} \) hay \(3\;\overrightarrow v + 3\;\overrightarrow u = \overrightarrow {OC} \)
\( \Rightarrow 3\left( {\overrightarrow v + \overrightarrow u } \right) = 3\;\overrightarrow v + 3\;\overrightarrow u \)

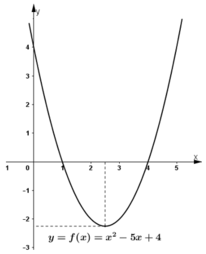
Hình a) có Δ > 0 ⇒ f(x) cùng dấu với a khi x nằm ngoài khoảng hai nghiệm của phương trình f(x) = 0; f(x) trái dấu với a khi x nằm trong khoảng hai nghiệm của phương trình f(x) = 0.
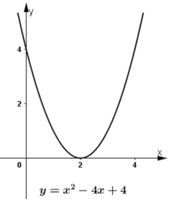
Hình b) có Δ = 0 ⇒ f(x) cùng dấu với a, trừ khi x = - b/2a.
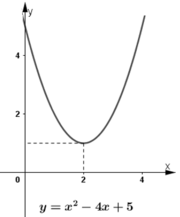
Hình c) có Δ < 0 ⇒ f(x) cùng dấu với a.

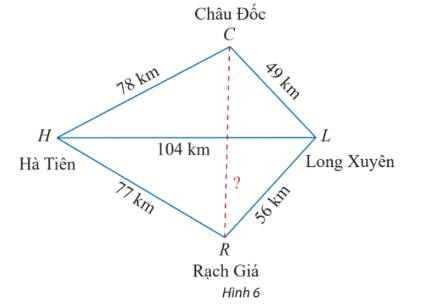
Bước 1: Áp dụng hệ quả của định lí cosin trong tam giác HCL, ta có:
\(\begin{array}{l}\cos \;\widehat {CHL} = \frac{{C{H^2} + H{L^2} - C{L^2}}}{{2.CH.HL}} = \frac{{{{78}^2} + {{104}^2} - {{49}^2}}}{{2.78.104}} = \frac{{4833}}{{5408}}\\ \Rightarrow \;\widehat {CHL} \approx {26^o}39'40,05''\end{array}\)
Áp dụng hệ quả của định lí cosin trong tam giác HLR, ta có:
\(\begin{array}{l}\cos \;\widehat {LHR} = \frac{{H{L^2} + H{R^2} - L{R^2}}}{{2.HL.HR}} = \frac{{{{104}^2} + {{77}^2} - {{56}^2}}}{{2.104.77}} = \frac{{13609}}{{16016}}\\ \Rightarrow \;\widehat {LHR} \approx {31^o}49'10,4''\\ \Rightarrow \;\widehat {CHR} \approx {58^o}28'50,45''\end{array}\)
Bước 2: Áp dụng định lí cosin \(C{R^2} = H{C^2} + H{R^2} - 2.HC.HR\cos \widehat {CHR}\)
\(\begin{array}{l} \Leftrightarrow C{R^2} = {78^2} + {77^2} - 2.78.77\cos {58^o}28'50,45''\\ \Rightarrow CR \approx 75,72\end{array}\)
Vậy khoảng cách giữa Châu Đốc và Rạch Giá là 75, 72 km.

A = {x < 20 | x thuộc N}
= {1 ; 2 ; 3 ; ... ; 19}
B = {x lẻ | x khác 0}
= {1 ; 3 ; 5 ; 7 ; ...}
\(A\subset N\)
\(B\subset N\)
A= {X<20|x thuộc N }
= {1;2;3...;19}
B= { x lẻ |x khác 0}
= { 1;3:5:7,...}
A€ N
B€ N

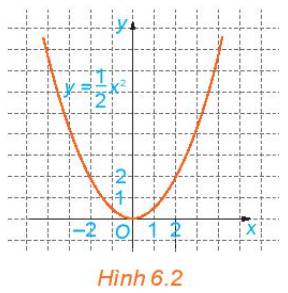
Dựa vào độ thị ta thấy (0; 0); (2; 2); (-2; 2) nằm trên đồ thị hàm số \(y = \frac{1}{2}{x^2}\)
Ta nhận ra được: \(\begin{array}{l}0 = \frac{1}{2}{.0^2}\\2 = \frac{1}{2}{.2^2}\\2 = \frac{1}{2}.{( - 2)^2}\end{array}\) Vì vậy những điểm có tọa độ \(\left( {x;\frac{1}{2}{x^2}} \right)\) sẽ nằm trên đồ thị.

Vì ABCD là hình bình hành nên \(\left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\), hay \(\overrightarrow {AD} = \overrightarrow {BC} \).
Do đó \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).




Dựa vào Atlat trang 6-7, dẫn chứng về mối quan hệ giữa độ nông –sâu, rộng – hẹp của thềm lục địa với vùng đồng bằng, đồi núi kế bên là:
- Ở các đồng bằng châu thổ Bắc Bộ và Nam Bộ, thềm lục địa khu vực vùng biển Bắc Bộ và Nam Bộ rộng, nông, thoải, các đường đẳng sâu thoải dần ra biển, diện tích khu vực có độ sâu dưới 200m rất lớn.
- Ở khu vực ven biển miền Trung, nhất là Nam Trung Bộ có núi ăn lan ra sát biển, thềm lục địa hẹp, dốc, các đường đẳng sâu đổ mau xuống độ sâu 2000m.