
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 0,24 | 1 | 9/4 | 4 | 25/4 | 9 |
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 0,24 | 1 | 9/4 | 4 | 25/4 | 9 |

a: \(a=\dfrac{y}{t^2}\left(t< >0\right)\)
Thay các giá trị đo, ta được:
\(\dfrac{1}{2^2}=\dfrac{4}{4^2}=\dfrac{1}{4}< >\dfrac{0.24}{1}\)
vì a=1/4 nên lần đo 1 sai
b: Đoạn đường lăn được 6,25m có nghĩa là y=6,25
\(\dfrac{1}{4}t^2=\dfrac{25}{4}\)
nên t=5
c: 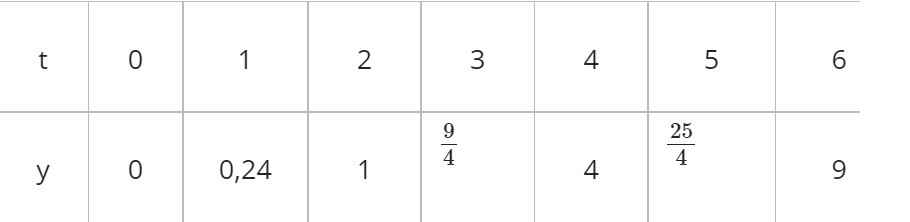

hay R = 10 Ω, t = 1s vào công thức Q = 0,24R I 2 t, ta có :
Q = 0,24.10. I 2 .1 = 2,4 I 2
Giá trị của Q được thể hiện trong bảng sau :
| I (A) | 1 | 2 | 3 | 4 |
| Q (calo) | 2,4 | 9,6 | 21,6 | 38,4 |

| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 1/2 x2 | 9/2 | 2 | 1/2 | 0 | 1/2 | 2 | 9/2 |
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = (-1)/2 x2 | (-9)/2 | -2 | (-1)/2 | 0 | (-1)/2 | -2 | (-9)/2 |

a) + Sau 1 giây, vật chuyển động được: s(2) = 4.22 = 16m
Vậy vật cách mặt đất: 100 – 4 = 96 (m).
+ Sau 2 giây, vật chuyển động được: s ( 2 ) = 4 . 2 2 = 16 m
Vậy vật cách mặt đất: 100 – 16 = 84 (m).
b) Vật tiếp đất khi chuyển động được 100m
⇔ 4 t 2 = 100 ⇔ t 2 = 25 ⇔ t = 5 .
Vậy vật tiếp đất sau 5 giây.

+ Điền vào ô trống:
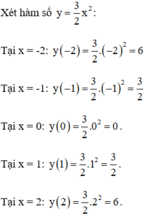
Vậy ta có bảng:
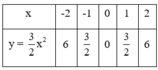
Tương tự như vậy với hàm số 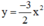 . Ta có bảng:
. Ta có bảng:
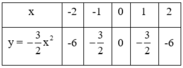
+ Vẽ đồ thị hàm số:
Trên mặt phẳng lưới lấy các điểm A(-2; 6); 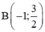 ; O(0; 0);
; O(0; 0); 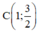 ; D(2; 6).
; D(2; 6).
Nối các điểm trên theo một đường cong ta được parabol 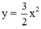
Lấy các điểm A’ (-2; -6); 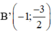 ; O(0; 0);
; O(0; 0); 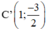 ; D’(2; -6).
; D’(2; -6).
Nối các điểm trên theo một đường cong ta được parabol 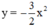
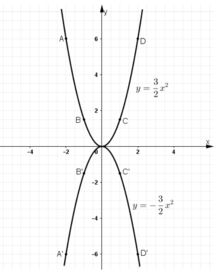
Nhận xét: Đồ thị hàm số 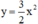 và
và 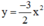 đối xứng nhau qua trục Ox.
đối xứng nhau qua trục Ox.

+ Sau 1 giây, vật chuyển động được: s(1) = 4.12 = 4m.
Vậy vật cách mặt đất: 100 – 4 = 96 (m).
+ Sau 2 giây, vật chuyển động được: s(2) = 4.22 = 16m
Vậy vật cách mặt đất: 100 – 16 = 84 (m).