

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




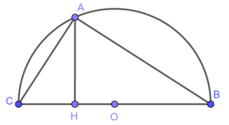
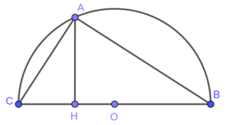
Đặt độ dài cạnh AB = x; điều kiện: x > 0
Theo bài ra theo điều (1) ta có: BC = x + 2a (3)
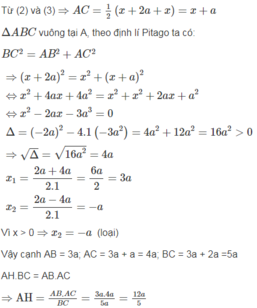

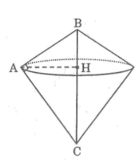
Khi quay tam giác ABC một vòng quanh cạnh huyền BC ta được hai hình nón có đáy úp vào nhau, bán kính đường tròn đáy bằng đường cao AH kẻ từ A đến cạnh huyền BC.
Trong tam giác vuông ABC ta có:


Ta có:
\(\frac{1}{AB}+\frac{1}{AC}+\frac{1}{AH}=1\)
\(\Leftrightarrow\frac{1}{AB^2}+\frac{1}{AC^2}+\frac{1}{AH^2}+\frac{2}{AB.AC}+\frac{2}{AC.AH}+\frac{2}{AB.AH}=1\)
\(\Leftrightarrow\frac{2}{AH^2}+\frac{2}{AH.BC}+\frac{2}{AC.AH}+\frac{2}{AB.AH}=1\)(Do \(\hept{\begin{cases}\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\\AB.AC=AH.BC\end{cases}}\)(Hệ thức lượng)
\(\Leftrightarrow\frac{2}{AH}\left(\frac{1}{AH}+\frac{1}{BC}+\frac{1}{AB}+\frac{1}{AC}\right)=1\)
\(\Leftrightarrow\frac{2}{AH}\left(1+\frac{1}{BC}\right)=1\)(Do \(\frac{1}{AB}+\frac{1}{AC}+\frac{1}{AH}=1\))
\(\Leftrightarrow\frac{BC+1}{BC}=\frac{AH}{2}\)
\(\Leftrightarrow2\left(BC+1\right)=AH.BC\)
\(\Leftrightarrow4BC+4=2AB.AC\)(Do AH.BC = AB.AC)
Kết hợp với Py-ta-go trong tam giác vuông ABC: \(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2+4BC+4=AB^2+2AB.AC+AC^2\)
\(\Leftrightarrow\left(BC+2\right)^2=\left(AB+AC\right)^2\)
\(\Leftrightarrow AB+AC=BC+2\)(Do \(\hept{\begin{cases}BC+2>0\\AB+AC>0\end{cases}}\))
Mà 3 cạnh AB,AC,BC là 3 cạnh nguyên lớn hơn 0
=> Chỉ có 2 cặp (AB,AC,BC) thỏa mãn: \(\left(3,4,5\right),\left(4,3,5\right)\)