Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tìm 1 số tự nhiên biết rằng khi xóa chữ số hàng đơn vị của số đó thì ta được số mới kém số phải tìm là 1808

Đặt các chữ cái vào các ô trống:
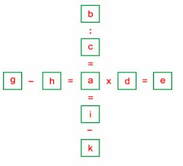
Theo đầu bài ta có các chữ cái khác nhau biểu thị các số khác nhau. Do đó: a ≠ 1; c ≠ 1; d ≠ 1; b > 1; e > 1. Vì 9 = 1 x 9 = 3 x 3 nên b ≠ 9 và e ≠ 9; và 7 = 1 x 7 nên b ≠ 7 và e ≠ 7.
Do đó: b = 6 và e = 8 hoặc b = 8 và e = 6.
Vì 6 = 2 x 3 và 8 = 2 x 4 nên a = b : c = e : d = 2.
Trong các ô trống a, b, c, d, e đã có các số 2, 3, 4, 6, 8; do đó chỉ còn các số 1, 5, 7, 9 điền vào các ô trống g, h, i, k.
* Nếu e = 6 thì g = 7 và h = 1. Do đó a = i - k = 9 - 5 = 42 (loại).
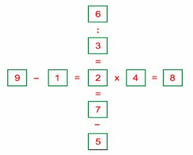
* Nếu e = 8 thì g = 9 và h = 1. Do đó a = i - k = 7 - 5 = 2 (đúng). Khi đó: b = 6 và c = 3. Kết quả:

9 + 8 + 76 + 5 + 4 - 3 + 2 - 1 = 100
Ủng hộ mk nha ^_-


\(\left(1+1+1\right)!=6\)
\(2+2+2=6\)
\(3\times3-3=6\)
\(\sqrt[]{4}+\sqrt{4}+\sqrt[]{4}=6\)
\(5+\left(5\div5\right)=6\)
\(6\times6\div6=6\)
\(7-\left(7\div7\right)=6\)
\(\sqrt{\left(8\div8\right)+8}!=6\)
\(\left(9-9\right)+\sqrt{9}!=6\)
\(\sqrt{10-\left(10\div10\right)}!=6\)
\(\left(9-9\right)+\sqrt{9}!=6\)


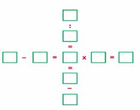
Bài toán chỉ có bốn cách điền như sau :
2 x 78 = 156 = 39 x 4
4 x 39 = 156 = 78 x 2
3 x 58 = 174 = 29 x 6
6 x 29 = 174 = 58 x 3