Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Điểm (-1 ; 1) thuộc đồ thị của hàm số ⇔ .
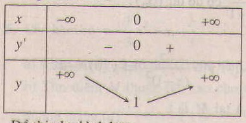
b) m = 1 . Tập xác định : R.
y' = 0 ⇔ x = 0.
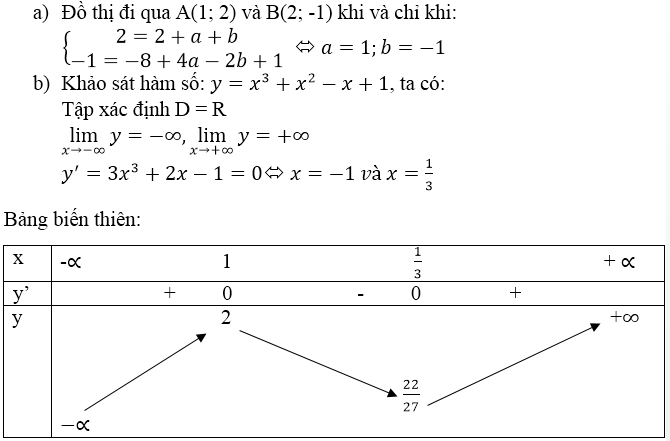
Bảng biến thiên:
Đồ thị như hình bên.
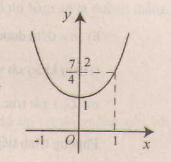
c) Vậy hai điểm thuộc (C) có tung độ
là A(1 ;
) và B(-1 ;
). Ta có y'(-1) = -2, y'(1) = 2.
Phương trình tiếp tuyến với (C) tại A là : y - = y'(1)(x - 1) ⇔ y = 2x -
Phương trình tiếp tuyến với (C) tại B là : y - = y'(-1)(x + 1) ⇔ y = -2x -
.

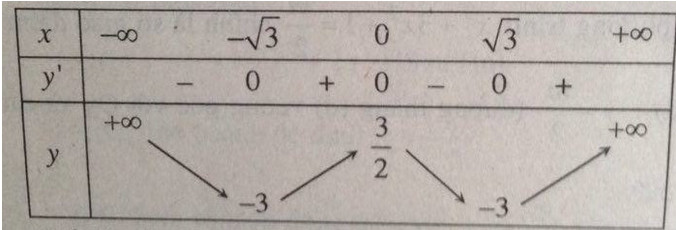
a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
Bảng biến thiên:
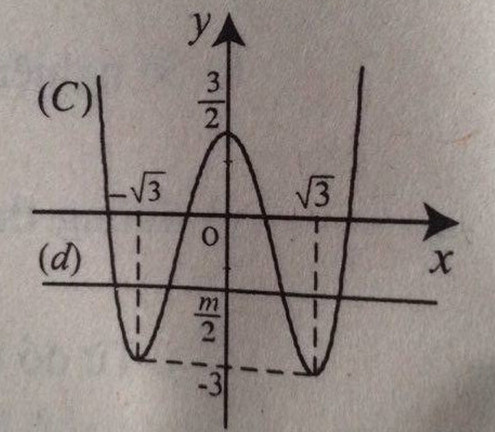
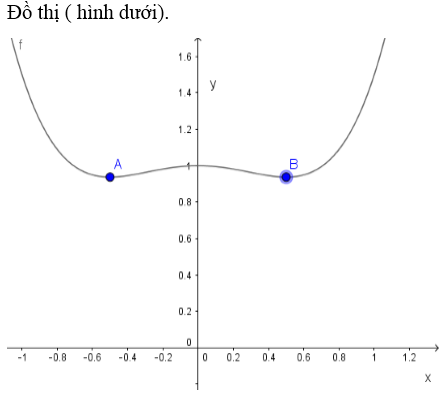
Đồ thị hàm số:
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm
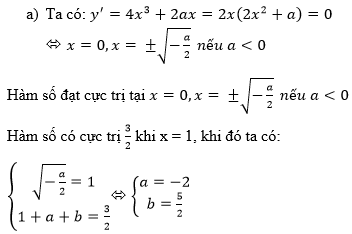

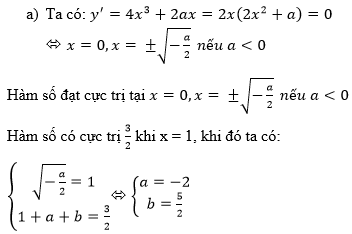


a.
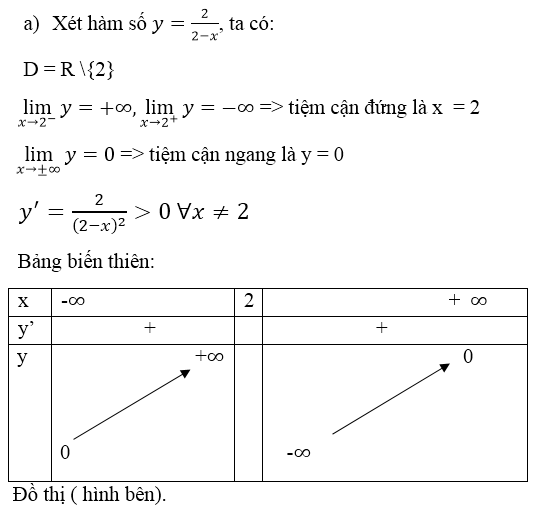
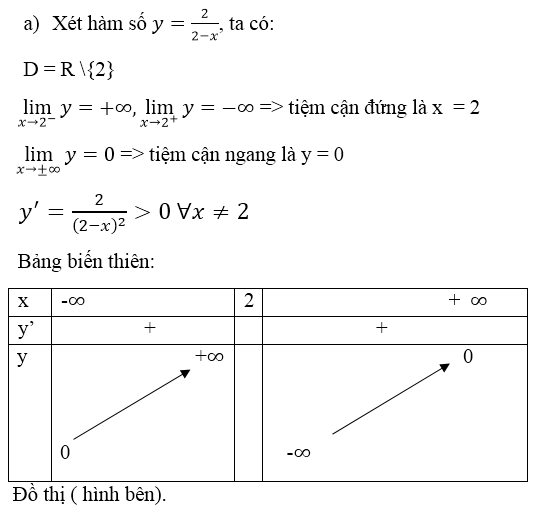
TXĐ: \(D=R\backslash\left\{-2\right\}\)
Sự biến thiên: \(y'=\dfrac{5}{\left(x+2\right)^2}>0\) ; \(\forall x\ne-2\)
\(\Rightarrow\) Hàm đồng biến trên các khoảng \(\left(-\infty;-2\right)\) và \(\left(-2;+\infty\right)\)
\(\lim\limits_{x\rightarrow-2}\dfrac{3x+1}{x+2}=\infty\Rightarrow x=-2\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow\infty}\dfrac{3x+1}{x+2}=3\Rightarrow y=3\) là tiệm cận ngang
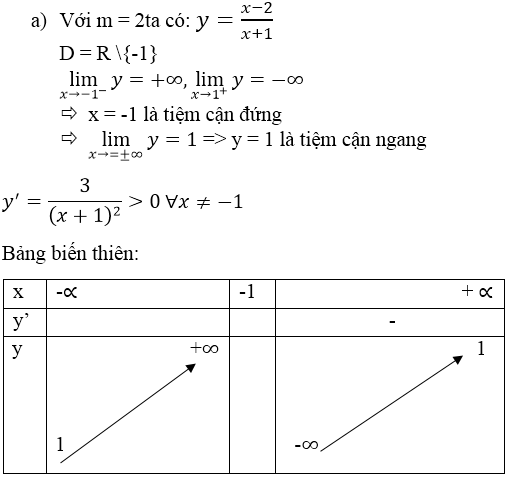
Bảng biến thiên:
x y' y -2 -vc +vc + + 3 +vc -vc 3
b.
\(y'\left(-1\right)=\dfrac{5}{\left(-1+2\right)^2}=5\) ; \(y\left(-1\right)=\dfrac{3.\left(-1\right)+1}{-1+2}=-2\)
Phương trình tiếp tuyến:
\(y=5\left(x+1\right)-2\Leftrightarrow y=5x+3\)