Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

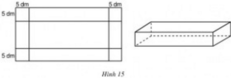
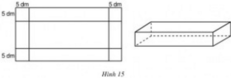
Gọi chiều rộng của miếng tôn là x(dm), x>10. Chiều dài của nó là 2x(dm).
Khi làm thành một cái thùng không đáy thì chiều dài của thùng là 2x-10(dm), chiều rộng là x-10 (dm), chiều cao laf5(dm).Dung tích của thùng là 5(2x-10)(x-10) d m 3
Theo đầu bài ta có phương trình:
5(2x-10)(x-10)=1500 hay x 2 - 15 x - 100 = 0
Giải phương trình: ∆ = 225 + 400 = 625 , ∆ = 25 ; x 1 = 20 , x 2 = - 5
Trả lời: Miếng tôn có chiều rộng bằng 20 (dm), chiều dài bằng 40(dm)

Nửa chu vi của tấm bìa là: 80 : 2 = 40 (cm)
Gọi chiều rộng của tấm bìa là x (0 < x < 20, cm)
Chiều dài của tấm bìa là 40 – x (cm)
Cắt bỏ 4 góc của tấm bìa rồi gập lại thành dạng hình hộp khi đó:
Chiều dài của hình hộp là: 40 – x – 6 = 34 – x (cm)
Chiều rộng của hình hộp là x – 6 (cm)
Chiều cao của hình hộp là 3 cm
Lúc này diện tích hình hộp chữ nhật bằng 339 c m 2 và bằng tổng diện tích xung quanh với diện tích một đáy của nó
Ta có phương trình:
[(34 – x + x – 6).2].3 + (34 – x)(x – 6) = 339
↔ 28.2.3 + 34x – 204 – x 2 + 6x = 339
↔ 168 + 40x – 204 – x 2 = 339 ↔ x 2 – 40x + 375 = 0
∆’ = ( − 20 ) 2 – 1.375 = 25 > 0
Phương trình có hai nghiệm
x 1 = 20 + 25 = 25 k t m
hoặc x 2 = 20 - 25 = 15 t m
Vậy tấm bìa ban đầu có kích thước chiều rộng là 15cm và chiều dài là
40 – 15 = 25cm
Đáp án: D

Đặt độ dài cạnh bát giác đều là \(a\left(cm\right),0< a< 1\)
Độ dài cạnh góc vuông của tam giác vuông bị cắt đi là: \(\frac{1-a}{2}\)(cm).
Độ dài cạnh huyền của tam giác vuông đó là: \(\frac{1-a}{2}.\sqrt{2}=\frac{1-a}{\sqrt{2}}\left(cm\right)\)
đó cũng chính là độ dài cạnh của bát giác đều.
Ta có: \(a=\frac{1-a}{\sqrt{2}}\)
\(\Leftrightarrow a=\sqrt{2}-1\)(thỏa mãn)
Độ dài cạnh góc vuông của tam giác vuông là:
\(\frac{1-\left(\sqrt{2}-1\right)}{2}=\frac{2-\sqrt{2}}{2}\)(cm)
Tổng diện tích của bốn tam giác vuông bị cắt đi là:
\(\frac{1}{2}\left(\frac{2-\sqrt{2}}{2}\right)^2.4=3-2\sqrt{2}\left(cm^2\right)\)