Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

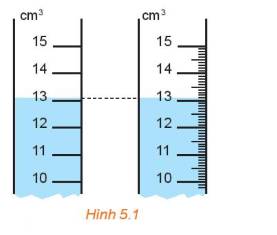
Giả sử ống nước thứ nhất là trang đo và ống nước thứ hai là Hòa đo.
Khi đó ống thứ nhất đo được là 13\(c{m^3}\), ống thứ hai là 13,1\(c{m^3}\)
Chú ý
Với ống thứ hai thì có vạch chia nhỏ hơn.

Ta quan sát hình trên thì thấy số 13,1 gần \(\bar a\) hơn.

Đặt x=B'C(km), 0<=x<=9
=>\(BC=\sqrt{x^2+36};AC=9-x\)
Chi phí xây dựng dường ống là:
\(C\left(x\right)=130000\sqrt{x^2+36}+50000\left(9-x\right)\left(USD\right)\)
Hàm C(x) xác định và liên tục trên [0;9] và \(C'\left(x\right)=10000\left(\dfrac{13x}{\sqrt{x^2+36}}-5\right)\)
C'(x)=0
=>13x=5 căn x^2+36
=>x=5/2

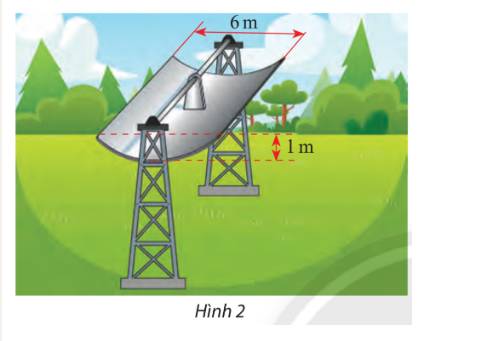
a) Vẽ lại parabol mô phỏng mặt cắt trên như hình dưới
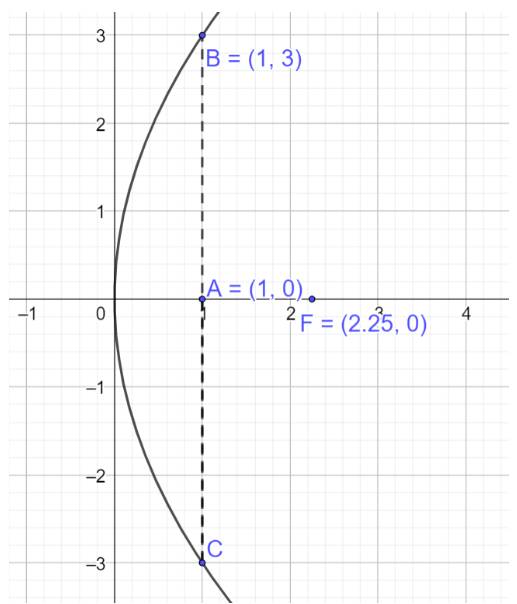
Ta có: \(OA = 1,BC = 2{y_B} = 6 \Rightarrow B\left( {1;3} \right)\)
Giả sử phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Thay tọa độ điểm B vào phương trình \({y^2} = 2px\) ta có: \({3^2} = 2p.1 \Rightarrow p = \frac{9}{2}\)
Vậy phương trình chính tắc của parabol mô phỏng mặt cắt trên là \({y^2} = 9x\)
b) Khoảng cách từ tâm đường ống đến đỉnh của parabol chính là độ dài từ đỉnh tới tiêu điểm của parabol
Từ phương trình chính tắc ta có tiêu điểm \(F\left( {\frac{9}{4};0} \right)\)
Vậy khoảng cách từ tâm đường ống đến đỉnh của parabol là \(\frac{9}{4}\) m

Theo đề bài ta thấy rằng:
1 ống ngắn có chiều dài bằng \(\frac{1}{80}\) đoạn đường
1 ống dài có chiều dài bằng \(\frac{1}{50}\) đoạn đường.
1 ống dài dài hơn 1 ống ngắn là:
\(\frac{1}{50}-\frac{1}{80}=\frac{3}{400}\) (đoạn đường.)
Giả sử dùng 62 ống dài để đặt ống dẫn nước, thì sẽ dư ra:
\(62x\frac{1}{50}-1=\frac{12}{50}\) (đoạn đường)
Do đó số ống ngắn là:
\(\frac{12}{50}:\frac{3}{400}=32\) (ống)
Số ống dài là:
62-32=30 (ống)
Đáp số: 30 ống dài
32 ống ngắn.