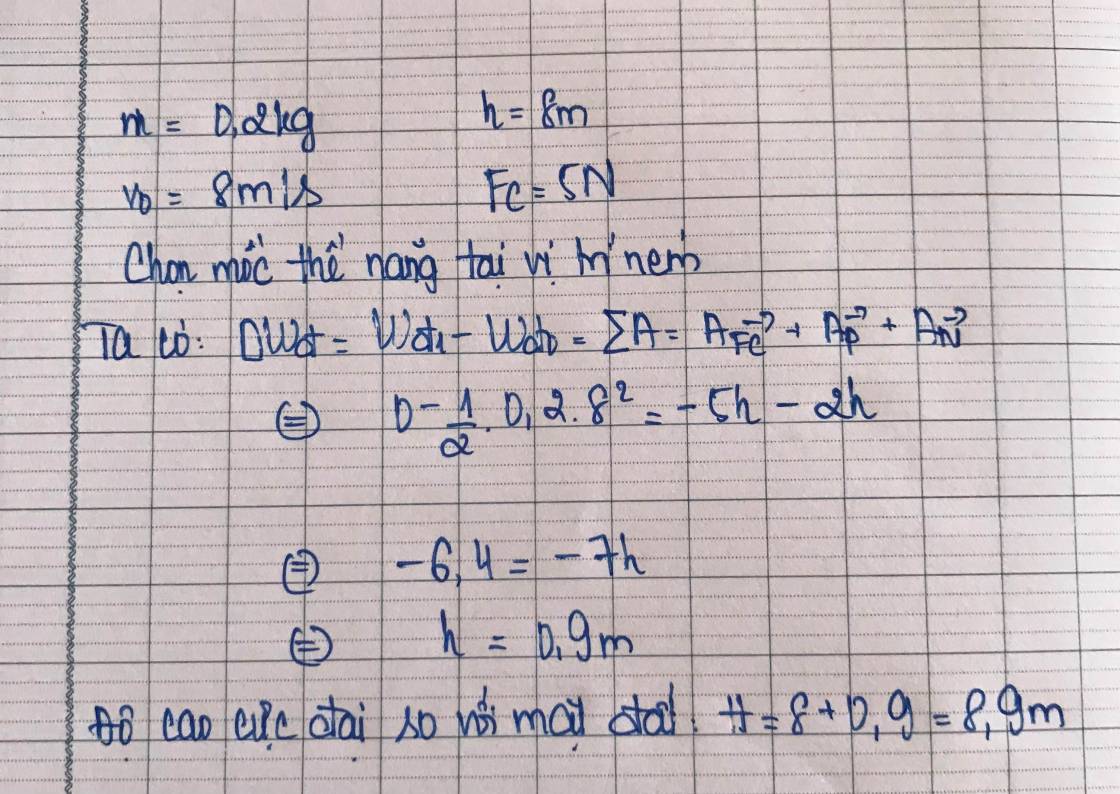Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

m=0,05kg vo=20m/s g=10m/s v1(tại độ cao cực đại)=0m/s
a) Lấy gốc thế năng tại mặt đất
Wđ1=\(\frac{1}{2}mv_o^2=\frac{1}{2}0,05.20^2=10\left(J\right)\)
Wt1=mgzo=0,05.10.0=0(J)
W1=10(J)
Wđ2=\(\frac{1}{2}mv_1^2=\frac{1}{2}0,05.0=0\left(J\right)\)
Áp dụng Định luật bảo toàn cơ năng ta có: W1 = W2 ⇔ 10= Wt2
⇒mgz2=10 ⇔ 0,05.10.z2=10 ⇒ z2=20(m)

lấy gốc thế năng tại mặt đất
a) gọi vị trí ban đầu là A
cơ năng tại A: \(W_A=W_{t_A}+W_{đ_A}=\)550J
b)gọi vị tại độ cao cực đại là B
cơ năng tại B: \(W_B=W_{t_B}+W_{đ_B}=m.g.h_B+0\)
bảo toàn cơ năng: \(W_A=W_B\)
\(\Rightarrow h_B=55m\)
c)gọi vị trí tại mặt đất là C
cơ năng tại C: \(W_C=W_{t_C}+W_{đ_C}=0+\frac{1}{2}.m.v_C^2\)
bảo toàn cơ năng: \(W_A=W_C\)
\(\Rightarrow v_C=\)\(10\sqrt{11}\)m/s
d) gọi vị trí mà động năng bằng \(\frac{3}{5}\) cơ năng là D \(\left(W_{đ_D}=\frac{3}{5}W_{t_D}\right)\)
cơ năng tại D: \(W_D=W_{t_D}+W_{đ_D}=\frac{8}{3}W_{đ_D}\)
bảo toàn cơ năng: \(W_A=W_D\)
\(\Rightarrow v_D=\frac{5\sqrt{66}}{2}\)m/s
e) gọi vị trí cách mặt đất 40m là E
cơ năng tại E: \(W_E=W_{đ_E}+W_{t_E}\)
bảo toàn cơ năng: \(W_A=W_E\)
\(\Rightarrow v_E=\)\(10\sqrt{3}\)m/s
f) gọi vị trí mà vật đạt độ vận tốc 20m/s là F
cơ năng tại F: \(W_F=W_{t_F}+W_{đ_F}\)
bảo toàn cơ năng: \(W_A=W_F\)
\(\Rightarrow h_F=35m\)
g) công của trọng lực
\(A_P=P.s=10.50=500J\)
h) cơ năng tại B lúc này :\(W'_B=0+W_{t_B}=m.g.h'_B\)
công của lực cản bằng biến thiên động năng
\(A_{F_c}=W'_B-W_A\) (\(s=h'_B-10\))
\(\Leftrightarrow F_c.s.cos180^0=W'_B-W_A\)
\(\Rightarrow h'_B\approx\)23,846m

a) Ta có luật bảo toàn năng lượng cơ học:
Động năng ban đầu + Thế năng ban đầu = Động năng cuối + Thế năng cuối
Ta có thể tính khả năng ban đầu và chức năng ban đầu của vật:
Thế năng ban đầu = mgh = 0 (vì chọn gốc thế năng ở mặt đất) Động năng ban đầu = (1/2)mv^2 = (1/2)m(20)^2 = 200m
Theo yêu cầu của đề bài, ta cần tìm vận tốc của vật khi hoạt động = 3 lần thế năng. Tốc độ tìm kiếm call is v.
Ta có:
(1/2)mv^2 = 3mgh
Với h = 0 (do chọn gốc thế năng ở mặt đất), ta có:
(1/2)mv^2 = 0 ⇒ v = 0
Do đó vận tốc của vật thể đang hoạt động bằng 3 lần thế năng là 0.
b) Ta sẽ giải quyết bài toán bằng cách định mức các biến thiên động. Theo lý do này, tổng hợp các lực lượng bên ngoài bằng các biến thiên của năng lượng cơ học.
Gọi h là tốc độ cao cần tìm, v là vận tốc của vật khi ở tốc độ cao đó.
Lực mạnh Fg = mg hướng xuống dưới, lực cản Fc = 0,5mg hướng ngược lại với chiều đi lên.
Tổng cộng các lực lượng bên ngoài trong quá trình vật liệu đi từ mặt đất lên độ cao bằng:
W = ∆K = K cuối - Kđầu = (1/2)mv^2 - 0 = (1/2)mv^2
Tổng cộng các lực lượng bên ngoài trong quá trình vật liệu đi từ độ cao h xuống mặt đất bằng:
W' = ∆U = Uđầu - U cuối = mgh - 0 = mgh
Do vật thể đi từ mặt đất lên độ cao h rồi rơi xuống mặt đất, nên tổng công lực bên ngoài trong quá trình vật thể đi từ mặt đất đến mặt đất bằng 0.
Theo định lý về biến thiên chức năng, ta có:
W + W' = 0 ⇒ (1/2)mv^2 + mgh = 0 ⇒ h = - v^2/2g = -200/20 = -10 (không có ý nghĩa vật lý)
Vì vậy, không có độ cực đại cao khi lực cản bằng 0,5 lần trọng lượng.

a) Thế năng trọng trường tại vị trí ném: \(W_{t1}=mgh_1=2.10.10=200(J)\)
Động năng: \(W_{đ1}=\dfrac{1}{2}mv^2=\dfrac{1}{2}.2.20^2==400(J)\)
Ở độ cao cực đại thì thế năng bằng cơ năng \(\Rightarrow W_{t2}=W=W_{đ1}+W_{t1}=400+200=600(J)\)
Lúc chạm đất, h = 0 \(\Rightarrow W_t=0\)
Sau khi ném 1s, độ cao của vật đạt được: \(h=10+20.1-\dfrac{1}{2}.10.1^2=25m\)
Thế năng lúc này: \(W_{t3}=m.g.h=2.10.25=500(J)\)
b) Độ cao cực đại của vật: \(h_{max}=\dfrac{W}{mg}=\dfrac{600}{2.10}=30(m)\)
Công của trọng lực từ lúc ném đến khi thế năng cực đại là: \(A_1=-2.10.(30-10)=400(J)\)
Công của trọng lực từ lúc ném đến khi chạm đất: \(A_2=2.10.10=200(J)\)

Gọi gia tốc đoàn tàu là: a = v 2 − v 0 2 t
với v = 20 ( m / s ) ; v 0 = 15 ( m / s ) s = 2 ( k m ) = 2000 ( m ) ⇒ a = 20 2 − 15 2 2.200 = 0 , 04 ( m / s 2 )
Gọi F → là lực kéo đầu máy và F → m s là lực ma sát lên đoàn tàu
Ta có: F → + F m s → + P → + N → = m a → ⇒ F − F m s = m a → F = F m s + m a .
Với Fms = N = P = mg. F = m( .g + a) = 8900N.
Thời gian tàu chạy từ A đến B là:
t = v 2 − v 1 a = 20 − 15 0 , 04 = 125 ( s )
Công của đầu máy trên đoạn đường AB: A = F.s = 17800000 ( J )
Công suất trung bình của đầu máy trên đoạn đường AB:
℘ ¯ = A t = 178.10 5 125 = 142400 W = 142 , 4 ( k W )

+ Gọi gia tốc của đoàn tàu: a = v 2 − v 0 2 t
+ v = 20 m / s v 0 = 15 m / s s = 2 k m = 2000 m ⇒ a = 20 2 − 15 2 2.200 = 0 , 04 m / s 2
+ Gọi F → là lực kéo của đầu máy và F → m s là lực ma sát trên đoàn tàu:
F → + F → m s + P → + N → = m a → ⇒ F − F m s = m a ⇒ F = F m s + m a
Với
F m s = μ N = μ P = μ m g ⇒ F = m μ . g + a = 8900 N
+ Thời gian tàu chạy từ A đến B là:
t = v 2 − v 1 a = 20 − 15 0 , 04 = 125 s
+ Công của đầu máy trên đoạn đường AB: A = F . s = 17800000 ( J )
+ Công suất trung bình của đầu máy trên đoạn đường AB:
ϑ ¯ = A t = 178.10 5 125 = 142400 W = 142 , 4 k W
Chọn đáp án A

Đáp án C
Sau khi hãm tốc :
Quãng đường tàu thứ nhất đã đi được đến khi dừng là
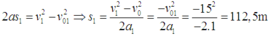
Quãng đường tàu thứ hai đã đi được đến khi dừng là
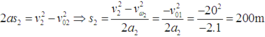
Suy ra, khoảng cách giữa hai tàu là 500 – 112,5 – 200 = 187,5m

Chọn mốc thế năng tại mặt đất
a. Cơ năng của vật tại vị trí ném. Gọi A là vị trí ném
v A = 8 ( m / s ) ; z A = 4 ( m )
W A = 1 2 m v A 2 + m g z A = 1 2 .0 , 1.8 2 + 0 , 1.10.4 = 7 , 2 ( J )
b. B là độ cao cực đại v B = 0 ( m / s )
Theo định luật bảo toàn cơ năng:
W A = W B ⇒ 7 , 2 = m g z B ⇒ z B = 7 , 2 0 , 1.10 = 7 , 2 ( m )
c. Gọi C là mặt đất z C = 0 ( m )
Theo định luật bảo toàn cơ năng
W A = W C ⇒ 7 , 2 = 1 2 m v C 2 ⇒ v C = 7 , 2.2 m = 7 , 2.2 0 , 1 = 12 ( m / s )
d. Gọi D là vị trí để vật có động năng bằng thế năng
W A = W D ⇒ W A = W d + W t = 2 W t ⇒ 7 , 2 = 2 m g z D ⇒ z D = 7 , 2 2 m g = 7 , 2 2.0 , 1.10 = 3 , 6 ( m )
e. Gọi E là vị trí để W d = 2 W t
Theo định luật bảo toàn năng lượng
W A = W E ⇒ W A = W d + W t = 3 2 W d ⇒ 7 , 2 = 3 2 . 1 2 m v E 2 ⇒ v E = 7 , 2.4 3. m = 28 , 8 3.0 , 1 = 4 6 ( m / s )
f. Gọi F là vị trí của vật khi vật ở độ cao 6m
Theo định luật bảo toàn năng lượng
W A = W F ⇒ W A = W d + W t = 1 2 m v F 2 + m g z F ⇒ 7 , 2 = 1 2. .0 , 1. v F 2 + 0 , 1.10.6 ⇒ v F = 2 6 ( m / s )
g.Gọi G là vị trí để vận tốc của vật là 3m/s
Theo định luật bảo toàn năng lượng
W A = W G ⇒ W A = W d + W t = 1 2 m v G 2 + m g z G ⇒ 7 , 2 = 1 2 .0 , 1.3 2 + 0 , 1.10. z G ⇒ z G = 6 , 75 ( m )
h. Gọi H là vị trí mà vật có thể lên được khi vật chịu một lực cản F = 5N Theo định lý động năng A = W d H − W d A
⇒ − F . s = 0 − 1 2 m v A 2 ⇒ s = m v A 2 F = 0 , 1.8 2 5 = 1 , 28 ( m )
Vậy độ cao của vị trí H so với mặt đất là 4+1,28 =5,28m