Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn: D
Hướng dẫn:
Tam giác ABM là tam giác đều cạnh a = 30 (cm) = 0,3 (m).
- Cường độ điện trường do q 1 = 2 . 10 - 2 (μC) = 2. 10 - 8 (C) đặt tại A, gây ra tại M là
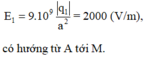
- Cường độ điện trường do q 2 = - 2 . 10 - 2 (μC) = - 2. 10 - 8 (C) đặt tại B, gây ra tại M là

- Cường độ điện trường tổng hợp tại điểm M là


Đáp án: C
Để cường độ điện trường tại M bằng 0 thì hai vecto E 1 do q1 gây ra và E 2 do q2 gây ra phải ngược chiều và cùng độ lớn nên M nằm trên đường thẳng AB và ngoài đoạn AB
Do |q2| > |q1| nên r1 < r2 => r1 = r2 - AB,
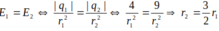
=>![]()


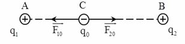
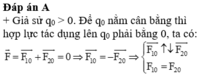


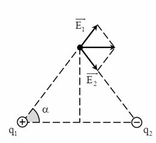

Cường độ điện trường bằng 0 khi:
\(\begin{array}{l}\overrightarrow {{E_1}} + \overrightarrow {{E_2}} = \overrightarrow E = \overrightarrow 0 \Rightarrow \overrightarrow {{E_1}} = - \overrightarrow {{E_2}} \\ \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \\{E_1} = {E_2}\end{array} \right.\end{array}\)
Vì \(\left| {{q_1}} \right| < \left| {{q_2}} \right| \Rightarrow \)Điểm đó thuộc đường thẳng AB và ngoài đoạn AB, gần A hơn (r2>r1)
\(\begin{array}{l}\left\{ \begin{array}{l}{r_2} - {r_1} = AB\\\frac{{r_1^2}}{{r_2^2}} = \frac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}} = \frac{{\left| {{{3.10}^{ - 6}}} \right|}}{{\left| { - 3,{{5.10}^{ - 6}}} \right|}}\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}{r_1} = 3,6m\\{r_2} = 4,2m\end{array} \right.\end{array}\)
Vậy điểm cần tìm cách A 3,6 m và cách B 4,2 m