Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
Phương pháp: Sử dụng bất đẳng thức Cosi để đánh giá giá trị của P.
Ta luôn có
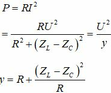
Theo bất đẳng thức Cosi ta có:
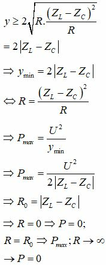

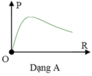
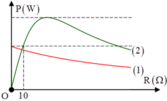
Từ các kết quả trên ta thấy đồ thị A chính là đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ trên mạch vào biến trở R.
Đáp án A

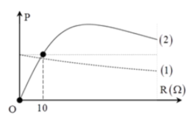
Ta có P 1 = U 2 R + r R + r 2 + Z L − Z C 2
Dạng đồ thị cho thấy rằng r > Z L − Z C = 30 Ω
P 1 = U 2 R R 2 + Z C 2
P 1 R = 0 = P 2 R = 10 ⇔ r r 2 + 30 2 = 10 10 2 + 30 2 ⇒ r = 90 Ω
Đáp án D

Đáp án D
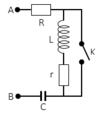
+ Cảm kháng của tụ điện Z L = L ω = 120 Ω
Hai giá trị của R cho cùng công suất
![]()

Đáp án D
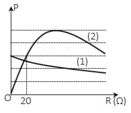
Vì LCω2 = 2 => ZC = 2ZL
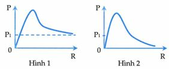
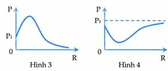
Xét đồ thị (2): 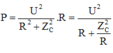
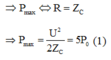 (1)
(1)
Khi R = 20Ω: 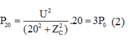 (2)
(2)
Từ (1) và (2) => ZC = 60Ω
Xét đồ thị (1): Khi R = 0: 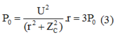 (3)
(3)
Từ (1) và (3) tìm được r = 180Ω.

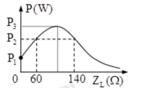
- Từ đồ thị ta thấy có hai giá trị của ZL là 60Ω và 140Ω cùng cho 1 giá trị P.
- Vị trí P3 đạt cực đại ứng với trường hợp cộng hưởng điện ZL = ZC
- Và có mối quan hệ giữa ZL3 với ZL1 và ZL2 là:
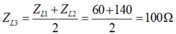
- Khi ZL = 0 thì mạch có công suất P1 thỏa mãn P3 /P1 = 3. Ta có:
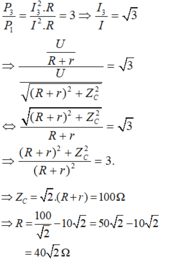

Chọn B.
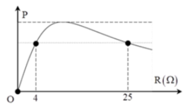
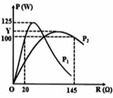
Hai đồ thị giao nhau tại R = a khi đó P 1 = P 2
Tại R = 20 Ω và R = a có cùng công suất nên:
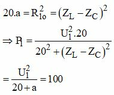 (1)
(1)
Tại R = a và R = 145 Ω có cùng công suất tương tự
⇒ P = 2 U 2 2 145 + a = 100 (2)
Mà
P 1 max = U 1 2 2 Z L − Z C = U 1 2 2 20 a = 125 (2); P 2 max = U 2 2 2 145 a (4)
Từ (2), (3) suy ra a = 80, U 1 = 100V. Thay vào (2) suy ra U 2 = 150 V
Thay vào (4) suy ra P 2 m a x = 104,5 W.
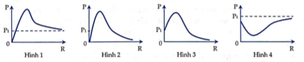
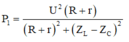
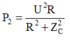
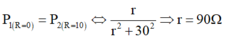

Đáp án D
Phương pháp: Sử dụng bất đẳng thức Cosi để đánh giá giá trị của P
Ta luôn có:
Theo bất đẳng thức Cosi ta có: