Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
Để đo được tần số của sóng âm và tốc độ truyền âm ta cần có các dụng cụ đo chuyên dụng. Ví dụ như tần số của âm thoa, hay các loại nhạc cụ thì cần có các bộ dụng cụ trong phòng thí nghiệm, dao động kí điện tử. Các loại âm thanh có tần số không xác định được phát ra từ các động cơ, máy khoan thì cần có các dụng cụ đo chuyên dụng hơn và cần sử dụng các công thức về năng lượng âm, mức cường độ âm để xác định.

Tham khảo:
* Đề xuất phương án thí nghiệm
Dụng cụ
(1) Máy phát âm tần,
(2) loa nhỏ,
(3) ống cộng hưởng là ống nhựa trong suốt (rải đều các hạt xốp trong lòng ống).
Thiết kế phương án thí nghiệm
Tìm hiểu công dụng của từng dụng cụ đã cho. Thiết kế phương án thí nghiệm đo tần số của âm do âm thoa phát ra bằng các dụng cụ này.

Tiến hành
– Đặt loa ở một đầu ống, loa nối với máy phát âm tần.
– Điều chỉnh để ống có chiều dài ngắn nhất.
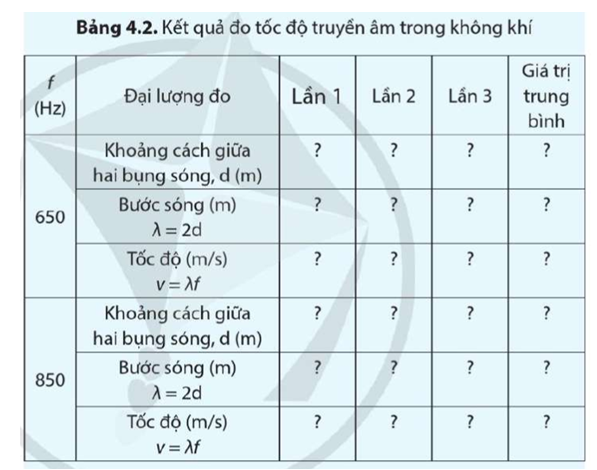
– Điều chỉnh để máy phát âm tần phát ra tần số f = 650 Hz và biên độ âm thanh không quá to.
– Thay đổi từ từ chiều dài ống sao cho tại đầu ống không đặt loa, có các vị trí mà các hạt xốp dồn lại nhiều nhất. Đó là các bụng sóng. Ghi lại khoảng cách giữa hai vị trí liên tiếp được xác định là bụng sóng. Thực hiện lại từ bước 3 với âm thanh có tần số f = 850 Hz.
– Ghi kết quả vào vở theo mẫu Bảng 4.2.
* Giải thích một số câu hỏi liên quan:
– Một đầu của ống cộng hưởng cần dịch chuyển vì cần thay đổi chiều dài của cột khí trong ống cộng hưởng. Phương án thay đổi độ dài cột khí trong ống bằng cách sử dụng một pittong ở đầu ống, di chuyển pittong sẽ gián tiếp thay đổi chiều dài cột khí.
– Cần xác định các vị trí mà âm thanh thu được có cường độ nhỏ nhất hoặc lớn nhất vì để xác định được ở đó là bụng sóng hay nút sóng và từ đó tính được bước sóng, tốc độ truyền âm, ….
– Để tính bước sóng của sóng âm qua các giá trị độ dài cột khí trong ống của những lần xác định được vị trí nút sóng, ta sử dụng công thức: \(L=\left(2k+1\right)\dfrac{\lambda}{4}\)

Hai thí nghiệm này cho ra kết quả khác nhau
Khoảng thời gian đo được khi thả rơi tự do vật từ độ cao 2,2m là 0,462s, tốc độ đo khi thả rơi vật là tốc độ rơi tự do của vật không phải tốc độ truyền âm trong không khí.

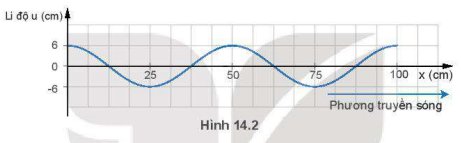
a) Từ đồ thị ta có bước sóng:
\(\lambda=50\left(cm\right)=0,5\left(m\right)\)
b) Chu kì 1s
\(\Rightarrow f=1Hz\)
Tốc độ truyền sóng:
\(v=\lambda f=0,5\cdot1=0,5\left(m/s\right)\)
c) Tần số tăng lên 5 Hz và tốc độ truyền sóng không đổi thì bước sóng mới là
\(\lambda_m=\dfrac{v}{f_m}=\dfrac{0,5}{5}=0,1\left(m\right)\)

Vận tốc truyền âm trong môi trường được so sánh như sau:
\(v_{rắn}>v_{lỏng}>v_{khí}\)
Nên khi ta áp tai xuống đường ray (vật rắn) thì âm truyền tới nhanh hơn trong không khí.
Vậy khi áp tai xuống đường ray sẽ nghe thấy tiếng tàu hỏa từ xa mà ngay lúc đó không thể nghe thấy trong không khí.

Tham khảo:
Có nhiều cách để đo tốc độ truyền âm.
- Cách 1: Có thể thả rơi 1 vật xuống một giếng cạn, đo thời gian từ lúc thả rơi đến khi nghe thấy âm thanh từ dưới giếng phản xạ lại. Đo độ sâu của giếng và kết hợp với thời gian đo được (thời gian rơi + thời gian truyền âm) là sẽ tính được tốc độ truyền âm.
- Cách 2: Sử dụng dụng cụ thí nghiệm đo tốc độ truyền âm như hình dưới:

Tham khảo:
Ta có: \(\lambda=\dfrac{c}{f}\)
Bước sóng của sóng điện từ tương ứng với dải tần số là từ 0,115 m đến 0,353 m
Mắt chúng ta không thể nhìn thấy sóng này vì sóng này có bước sóng và tần số nằm ngoài khoảng ánh sáng nhìn thấy.

Từ công thức tính tốc độ sóng: v = λ f , ta thấy để đo tốc độ truyền âm trong không khí cần xác định được tần số của sóng âm f, bước sóng của sóng âm λ .
- Xác định tần số f bằng máy phát âm tần,
- Xác định bước sóng thông qua công thức: l = k λ 2 ⇒ λ = 2 l k với chiều dài sợi dây và số bụng sóng xác định được.

Phao cầu cá nhỏ lên cao 6 lần trong 4 s tương ứng với 5T nên ta có T = 0,8 s
Khoảng cách giữa hai đỉnh sóng liên tiếp là: λ = v.T = 0,5.0,8 = 0,4m
Dải tần số mà học sinh có thể nghe thấy từ 30 Hz đến 16000 Hz.
Nên bước sóng ngắn nhất của âm thanh trong không khí mà bạn học sinh đó nghe được ở tần số 16000Hz.
\(\lambda = \frac{v}{f} = \frac{{330}}{{16000}} \approx 0,02\)(m)