
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 2:
a: *Vẽ đồ thị
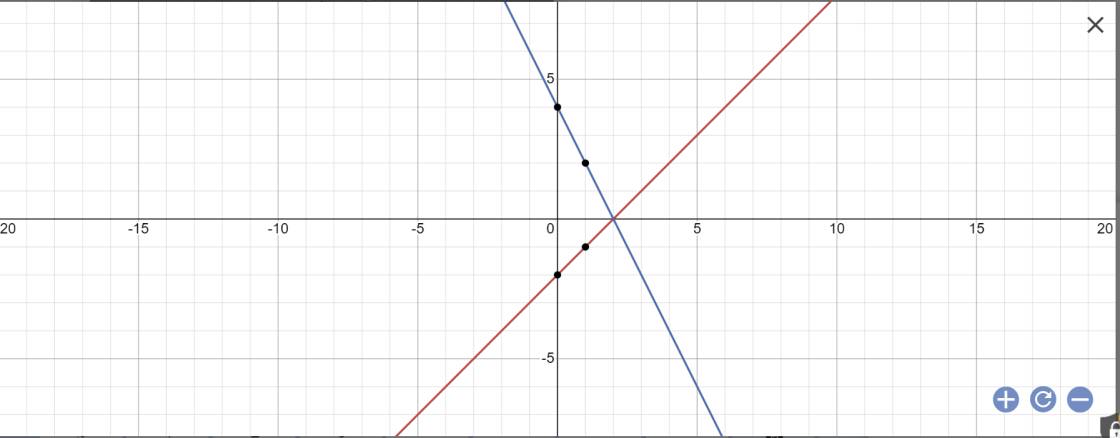
*Tìm giao điểm:
Phương trình hoành độ giao điểm là:
x-2=-2x+4
=>x+2x=4+2
=>3x=6
=>x=2
Thay x=2 vào y=x-2, ta được:
y=2-2=0
Vậy: (d1):y=x-2 cắt (d2): y=-2x+4 tại A(2;0)
b: *Vẽ đồ thị
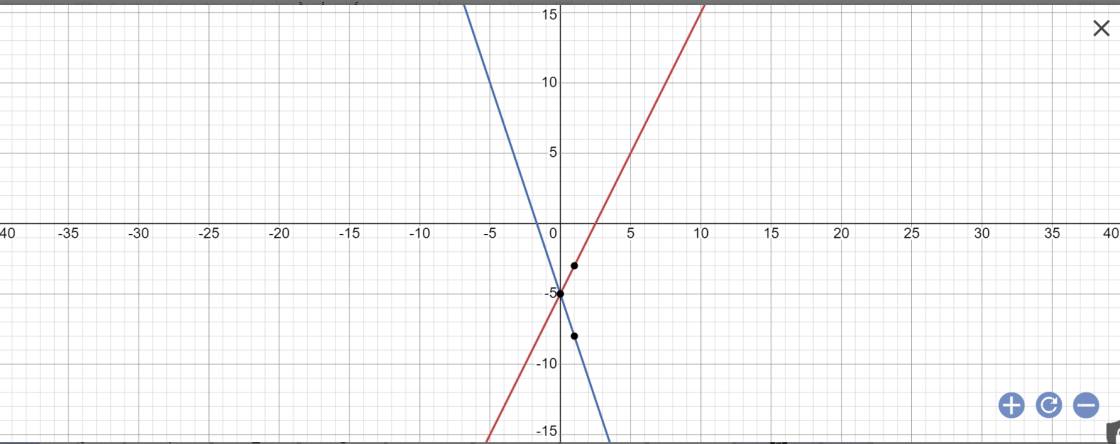
*Tìm giao điểm
Phương trình hoành độ giao điểm là:
2x-5=-3x-5
=>2x+3x=-5+5=0
=>5x=0
=>x=0
Thay x=0 vào y=2x-5, ta được:
\(y=2\cdot0-5=-5\)
Vậy: (d1): y=2x-5 cắt (d2):y=-3x-5 tại A(0;-5)
c: *Vẽ đồ thị
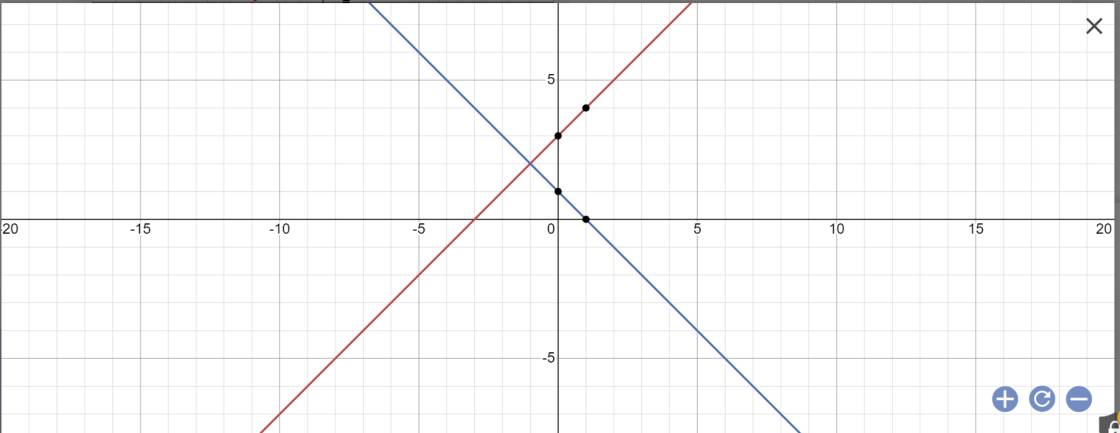
*Tìm giao điểm
Phương trình hoành độ giao điểm là:
x+3=-x+1
=>x+x=1-3
=>2x=-2
=>x=-1
Thay x=-1 vào y=x+3, ta được:
y=-1+3=2
vậy: (d1): y=x+3 và (d2): y=-x+1 cắt nhau tại C(-1;2)


\(a)P=\left(\dfrac{x^2+2}{x^3-1}+\dfrac{x+1}{x^2+x+1}+\dfrac{1}{1-x}\right).\left(\dfrac{x^2}{x+1}+1\right).\left(x\ne1;x\ne-1\right).\\ P=\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}.\dfrac{x^2+x+1}{x+1}.\\ P=\dfrac{x^2-x}{x-1}.\dfrac{1}{x+1}.\\ P=\dfrac{x\left(x-1\right)}{x-1}.\dfrac{1}{x+1}.\\ P=x.\dfrac{1}{x+1}.\\ P=\dfrac{x}{x+1}.\)
\(P=\dfrac{1}{4}.\Rightarrow\dfrac{x}{x+1}=\dfrac{1}{4}.\\ \Leftrightarrow4x-x-1=0.\\ \Leftrightarrow3x-1=0.\\ \Leftrightarrow x=\dfrac{1}{3}\left(TM\right).\)

A = ( x - 2 )2 + 5
= ( x - 2 ) 2 + 5 > hoặc = 5
=> GTNN là 5
B = x2+ 2x + 3
= x2 + 2 .x . 1 + 1 + 2
= ( x + 1 )2 + 2 >hoặc = 2
=> GTNN là 2
\(A=\left(x-2\right)^2+5\)
vì \(\left(x-2\right)^2\ge0\Rightarrow\left(x-2\right)^2+5\ge5\)
vậy min A=5 khi x=2
\(B=x^2+2x+3\)
\(=x^2+2x+1+2\)
\(=\left(x+1\right)^2+2\ge2\)
vậy Min B=2 khi x=-1

Để phân thức trên được xác định
Thì 16x2-25\(\ne\)0
=> (4x-5)(4x+5)\(\ne\)0
=> \(\begin{cases}4x-5\ne0\\4x+5\ne0\end{cases}\)
=>\(\begin{cases}4x\ne5\\4x\ne-5\end{cases}\)
=>\(\begin{cases}x\ne\frac{5}{4}\\x\ne\frac{-5}{4}\end{cases}\)
Vậy để phân thức trên được xác định thì \(x\ne\frac{5}{4}\) và \(x\ne\frac{-5}{4}\)

Vì \(AB//CD\) nên \(\left\{{}\begin{matrix}\widehat{B}+\widehat{C}=180^0\\\widehat{A}+\widehat{D}=180^0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\widehat{B}=\left(180^0+40^0\right):2=110^0\\3\widehat{D}=180^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{C}=180^0-110^0=70^0\\\widehat{D}=60^0\end{matrix}\right.\Rightarrow\widehat{A}=120^0\)
\(\widehat{B}=110^0\)
\(\widehat{C}=70^0\)
\(\widehat{A}=120^0\)
\(\widehat{D}=60^0\)

Câu 4:
a: ĐKXĐ: \(x\notin\left\{\dfrac{1}{2};-\dfrac{1}{2}\right\}\)
b: \(A=\dfrac{1-2x}{1-4x^2}\)
\(=\dfrac{1-2x}{\left(1-2x\right)\left(1+2x\right)}\)
\(=\dfrac{1}{2x+1}\)
c: Để A là số nguyên thì \(2x+1\inƯ\left(1\right)\)
=>\(2x+1\in\left\{1;-1\right\}\)
=>\(2x\in\left\{0;-2\right\}\)
=>\(x\in\left\{0;-1\right\}\)
Câu 3:
a: \(A=\dfrac{3x-2}{x}-\dfrac{x-7}{x-5}-\dfrac{10}{x^2-5x}\)
\(=\dfrac{3x-2}{x}-\dfrac{x-7}{x-5}-\dfrac{10}{x\left(x-5\right)}\)
\(=\dfrac{\left(3x-2\right)\left(x-5\right)-x\cdot\left(x-7\right)-10}{x\left(x-5\right)}\)
\(=\dfrac{3x^2-17x+10-x^2+7x-10}{x\left(x-5\right)}\)
\(=\dfrac{2x^2-10x}{x\left(x-5\right)}=\dfrac{2x\left(x-5\right)}{x\left(x-5\right)}=2\)

2,Có \(\widehat{A}+\widehat{D}=180^0\) (Hai góc trong cùng phía do AB//CD)
\(\Rightarrow\widehat{D}=180^0-115^0=65^0\)

 cứu em 2 câu này vs ạ
cứu em 2 câu này vs ạ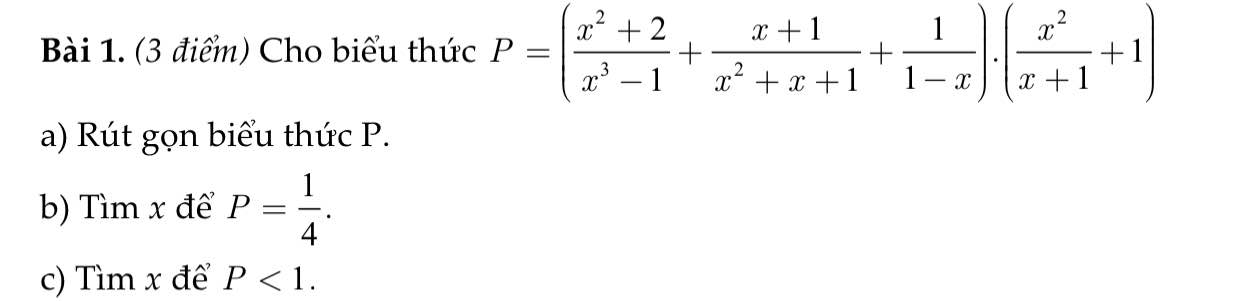
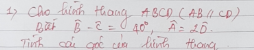
 giúp em 2 câu này vs ạ
giúp em 2 câu này vs ạ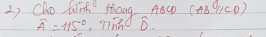
10:
a: =x^2+x+1/4+3/4=(x+1/2)^2+3/4>=3/4
Dấu = xảy ra khi x=-1/2
b: =x^2-3x+9/4-9/4
=(x-3/2)^2-9/4>=-9/4
Dấu = xảy ra khi x=3/2
c: =2x^2-10x+x-5
=2x^2-9x-5
=2(x^2-9/2x-5/2)
=2(x^2-2*x*9/4+81/16-121/16)
=2(x-9/4)^2-121/8>=-121/8
Dấu = xảy ra khi x=9/4
d: =x^2+2xy+y^2+4y^2-2*2y*1/2+1/4+2004,75
=(x+y)^2+(2y-1/2)^2+2004,75>=2004,75
Dấu = xảy ra khi y=1/4 và x=-1/4