K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 3 2022
Ta có \(\dfrac{a^3}{a^2+b^2}=a-\dfrac{ab^2}{a^2+b^2}\ge a-\dfrac{ab^2}{2ab}=a-\dfrac{b}{2}=\dfrac{2a-b}{2}\)(áp dụng cosi cho \(a^2+b^2\ge2ab\))
\(\dfrac{b^3}{b^2+1}=b-\dfrac{b}{b^2+1}\ge b-\dfrac{b}{2b}=b-\dfrac{1}{2}=\dfrac{2b-1}{2}\)(áp dụng cosi cho\(b^2+1\ge2b\))
\(\dfrac{1}{a^2+1}=1-\dfrac{a^2}{a^2+1}\ge1-\dfrac{a^2}{2a}=1-\dfrac{a}{2}=\dfrac{2-a}{2}\)( áp dụng cosi cho \(a^2+1\ge2a\))
Cộng vế theo vế
\(\dfrac{a^3}{a^2+b^2}+\dfrac{b^3}{b^2+1}+\dfrac{1}{a^2+1}\ge\dfrac{2a-b+2b-1+2-a}{2}\)\(\ge\dfrac{a+b+1}{2}\left(đpcm\right)\)
Dấu "=" xảy ra <=> a=b=1
16 tháng 9 2021
\(1,\\ ĐKXĐ:6-3x>0\Leftrightarrow-3x>-6\Leftrightarrow x< 2\)
\(2,A=\sqrt{5-2\sqrt{6}}-\sqrt{\left(\sqrt{2}-\sqrt{3}\right)^2}\\ A=\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}-\left|\sqrt{2}-\sqrt{3}\right|\\ A=\left|\sqrt{3}-\sqrt{2}\right|-\left(\sqrt{3}-\sqrt{2}\right)\\ A=\sqrt{3}-\sqrt{2}-\sqrt{3}+\sqrt{2}=0\)
29 tháng 12 2021
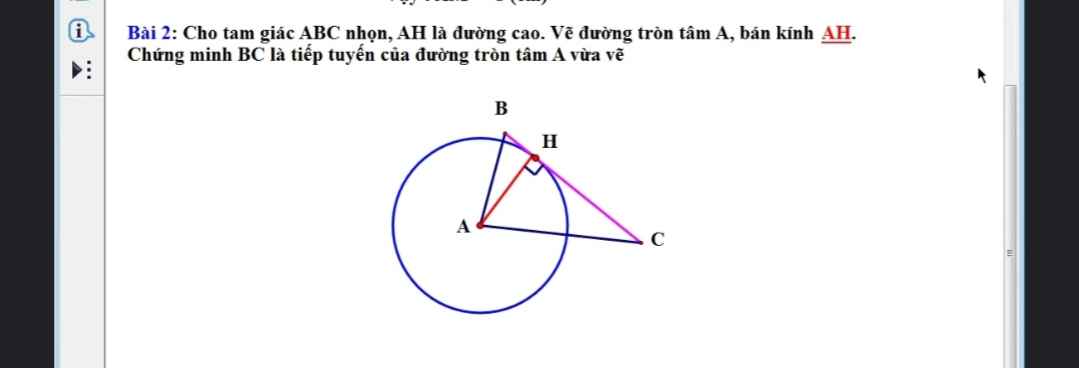
b: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
24 tháng 9 2021
c: Ta có: \(C=\sqrt{7-4\sqrt{3}}+\sqrt{7+4\sqrt{3}}\)
\(=2-\sqrt{3}+2+\sqrt{3}\)
=4
13 tháng 1 2023
a: \(=2\sqrt{2}+3\sqrt{2}-4\sqrt{2}=\sqrt{2}\)
b: \(=2\sqrt{5}+\sqrt{5}-1=3\sqrt{5}-1\)
c: \(=\dfrac{\sqrt{3}-1+\sqrt{3}+1}{2}-2\sqrt{3}=\sqrt{3}-2\sqrt{3}=-\sqrt{3}\)
d: =-căn 5
e: \(=\sqrt{3}-\sqrt{3}+1=1\)
k:=12-5*2=12-10=2
AH
Akai Haruma
Giáo viên
29 tháng 10 2023
Lời giải:
$x^2+y^2=z^2\Rightarrow (\frac{x}{z})^2+(\frac{y}{z})^2=1$
Đặt $\frac{x}{z}=a; \frac{y}{z}=b$ thì bài toán trở thành:
Cho $a,b>0$ thỏa mãn: $a^2+b^2=1$.
Tìm min $P=(1+\frac{1}{a})(1+\frac{1}{b})$
------------------
Có:
Áp dụng BĐT Cô-si: $1=a^2+b^2\geq 2ab$
$P=\frac{(a+1)(b+1)}{ab}=\frac{a+b+ab+1}{ab}=\frac{a+b+ab+a^2+b^2}{ab}$
$\geq \frac{2\sqrt{ab}+ab+2ab}{ab}$
$=\frac{2\sqrt{ab}+3ab}{ab}$
Vì $1\geq 2ab\Rightarrow 1\geq \sqrt{2ab}$
$\Rightarrow P\geq \frac{2\sqrt{2ab}.\sqrt{ab}+3ab}{ab}=\frac{(2\sqrt{2}+3)ab}{ab}=2\sqrt{2}+3$
Vậy $P_{\min}=2\sqrt{2}+3$
......
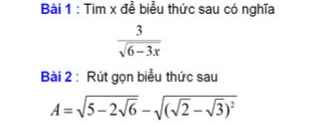
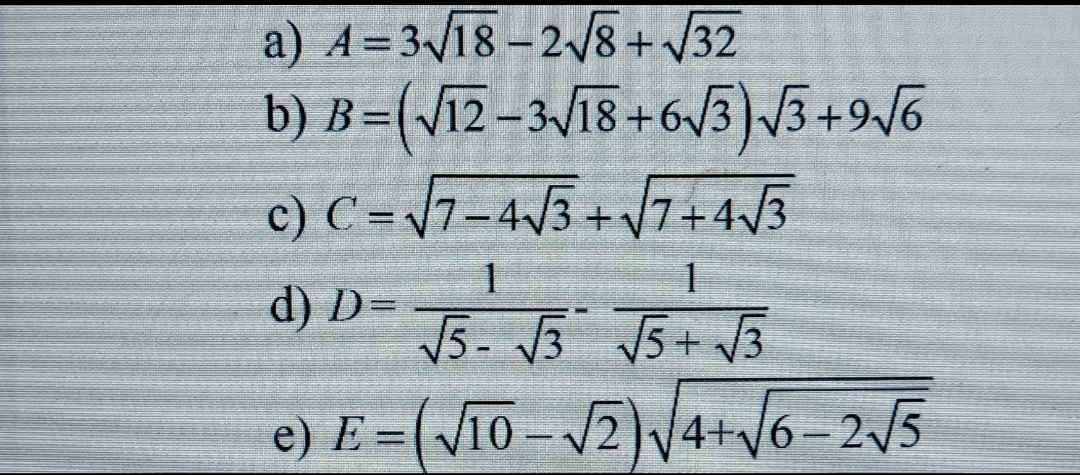