Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
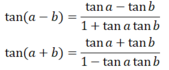
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
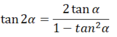
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích:
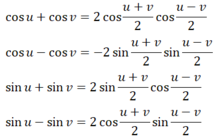

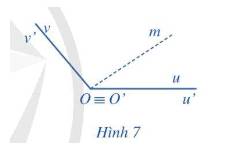
Quan sát Hình 7 ta thấy:
• Tia Om quay (chỉ theo chiều dương) xuất phát từ tia Ou đến trùng với tia Ov rồi quay tiếp một số vòng đến trùng với tia cuối Ov;
• Tia Om quay (chỉ theo chiều dương) xuất phát từ tia \(O'u' \equiv Ou\) đến trùng với tia \(O'v' \equiv Ov\)rồi quay tiếp một số vòng đến trùng với tỉa cuối \(O'v' \equiv Ov\).
Như vậy, sự khác biệt giữa hai góc lượng giác (Ou, Ov) và (O’u’, O’v’) chính là số vòng quay quanh điểm O. Vì vậy, sự khác biệt giữa số đo của hai góc lượng giác đó chính là bội nguyên của \({360^ \circ }\) khi hai góc đó tính theo đơn vị độ (hay bội nguyên của \(2\pi \) rad khi hai góc đó tính theo đơn vị radian).

Công thức tổng quát số đo của góc lượng giác \(\left(Ox,ON\right)=70^o+k\cdot360,k\in Z\)
Công thức tổng quát số đo của lượng giác
\(\left(Ox,OP\right)=\left(Ox,OM\right)+\left(OM,OP\right)=-50-120^o+m\cdot360^o=-170^o+m\cdot360^o,m\in Z\)

k ở đây được hiểu là "một số nguyên bất kì", giống hay khác nhau đều được
Ví dụ:
\(sinx=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Thì "k" trong \(\dfrac{\pi}{6}+k2\pi\) và "k" trong \(\dfrac{5\pi}{6}+k2\pi\) không liên quan gì đến nhau (nó chỉ là 1 kí hiệu, có thể k trên bằng 0, k dưới bằng 100 cũng được, không ảnh hưởng gì, cũng có thể 2 cái bằng nhau cũng được).
Khi người ta ghi 2 nghiệm đều là "k2pi" chủ yếu do... lười biếng (kiểu như mình). Trên thực tế, rất nhiều tài liệu cũ họ ghi các kí tự khác nhau, ví dụ 1 nghiệm là \(\dfrac{\pi}{6}+k2\pi\), 1 nghiệm là \(\dfrac{5\pi}{6}+n2\pi\) để tránh học sinh phát sinh hiểu nhầm đáng tiếc rằng "2 cái k phải giống hệt nhau về giá trị".

a. Mối liên hệ giữa các công thức:
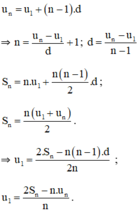
Dựa vào các công thức trên thấy cần phải biết ít nhất 3 đại lượng để tìm được các đại lượng còn lại.
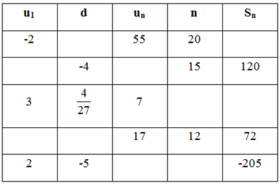
b. Ta có bảng:
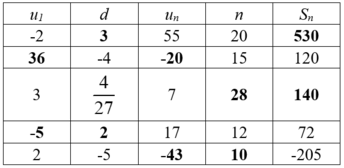
Giải thích:
+ Với u1 = -2; un = 55; n = 20
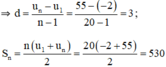
+ Với d = -4 ; n = 15 ; Sn = 120
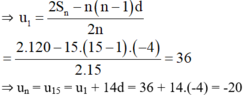
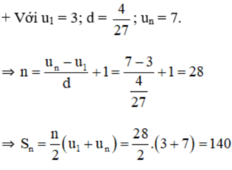
+ Với un = 17; n = 12; Sn = 72
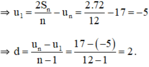
+ Với u1 = 2; d = -5; Sn = -205.
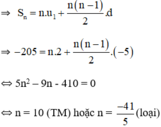
⇒ un = u10 = u1 + 9d = -43.

a: tìm được 1 giá trị duy nhất tương ứng của s
b: Có thể tìm được 2 giá trị tương ứng của t
c:
| s | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 16 |
| t | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |

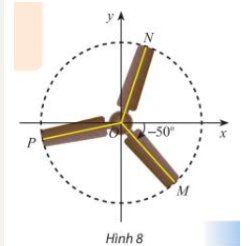
Vì mâm bánh xe ô tô được chia thành năm phần bằng nhau nên mỗi phần có số đo bằng \(\dfrac{360^o}{5}=72^o\)
Ta có: \(\left(ON,OM\right)=\left(ON,Ox\right)+\left(Ox,OM\right)\\ \Rightarrow\left(ON,Ox\right)=99^o\)
Công thức số đo tổng quát của góc lượng giác \(\left(ON,Ox\right)=99^o+k\cdot360^o,k\in Z\)


Công thức lượng giác cần nhớ
+ Về Hệ thức cơ bản
\(\sin^2\)\(a+\cos^2\)\(a=1\)
\(1+tg^2\)\(a=\frac{1}{\cos^2a}\) với \(a\ne\frac{\pi}{2}+k\pi\left(k\in Z\right)\)
\(t+cot\) \(g^2\)\(=\frac{1}{\sin^2a}\) với \(a\ne k\pi\)\(\left(k\in Z\right)\)
+ Về Phụ nhau và sai nhau(x2)
Phụ nhau: \(a\)và \(\frac{\pi}{2}-a\)
* Công thức:
\(\sin\left(\frac{\pi}{2}-a\right)=\cos a\)
\(\cos\left(\frac{\pi}{2}-a\right)=\sin a\)
\(tg\left(\frac{\pi}{2}-a\right)=\cot ga\)
\(\cot g\left(\frac{\pi}{2}-a\right)=tga\)
+ Về Sai nhau(x1): \(\frac{\pi}{2}:a\) và \(\frac{\pi}{2}+a\)
\(\sin\left(\frac{\pi}{2}+a\right)=\cos a\)
\(\cos\left(\frac{\pi}{2}+a\right)=-\sin a\)
\(tg\left(\frac{\pi}{2}+a\right)=-\cot ga\)
\(\cot g\left(\frac{\pi}{2}+a\right)=-tga\)
=> Từ Phụ nhau và sai nhau(x1), ta có công thức hợp thể như sau:
\(\sin\left(x+k\pi\right)=\left(-1\right)^k\)\(\sin x,k\in Z\)
\(\cos\left(x+k\pi\right)=\left(-1\right)^k\)\(\cos x,k\in Z\)
\(tg\left(x+k\pi\right)=tgx,k\in Z\)
\(\cot g\left(x+k\pi\right)=\cot gx\)
+ Về Sai nhau(x2): \(\pi:a\) và \(\pi+a\)
\(\sin\left(\pi+a\right)=-\sin a\)
\(\cos\left(\pi+a\right)=-\cos a\)
\(tg\left(\pi+a\right)=t\) \(ga\)
\(\cot g\left(\pi+a\right)=\cot ga\)
+ Về Đối nhau và Bù nhau:
*Công thức:
Đối nhau: \(a\) và \(-a\)
\(\sin\left(-a\right)=-\sin a\)
\(\cos\left(-a\right)=\cos a\)
\(tg\left(-a\right)=-tg\left(a\right)\)
\(\cot g\left(-a\right)=-\cot g\left(a\right)\)
Bù nhau: \(a\) và \(\pi-a\)
\(\sin\left(\pi-a\right)=\sin a\)
\(\cos\left(\pi-a\right)=-\cos a\)
\(tg\left(\pi-a\right)=-tga\)
\(\cot g\left(\pi-a\right)=-\cot ga\)
***************Chúc bạn học tốt**************
bn ko hỉu chỗ nào hỏi mik nhé