Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Công thoát: \(A=\dfrac{hc}{\lambda_0}=\dfrac{6,625.10^{-34}.3.10^8}{0,3.10^{-6}}=6,625.10^{-19}J=4,14MeV\)

Đáp án C
Cách giải
Áp dụng công thức tần số góc trong mạch dao động LC ta có
![]()

Phương pháp
Áp dụng công thức tính tần số góc trong mạch dao động ω = 1 L C
Cách giải
Áp dụng công thức tần số góc trong mạch dao động LC ta có
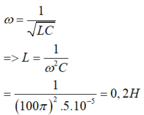
Đáp án C

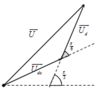
Biểu diễn vecto các điện áp.
Hiệu suất của động cơ H=A/P
→ P = A H = 8 , 5 0 , 85 = 10 kW.
→ Điện trở trong của động cơ R d c = P I 2 = 10000 50 2 = 4 Ω
→ Z d c = R cos 30 0 = 8 3 Ω.
→ U d c = I Z d c = 50 8 3 = 400 3 V.
Từ giản đồ vecto, ta thấy rằng góc hợp với U d c → và U d → là 150 độ .
→ U = 125 2 + 400 3 2 − 2.125. 400 3 cos 150 0 = 345 V
Đáp án B

Chọn đáp án C
+ Công suất tiêu thụ không đổi nên: ![]()
+ Hệ số công suất của cuộn dây: ![]()

\(Z_L=\omega L=100\sqrt{3}\Omega\)
C thay đổi để Uc max khi: \(Z_C=\frac{R^2+Z_L^2}{Z_L}=\frac{100^2+3.100^2}{100\sqrt{3}}=\frac{4}{\sqrt{3}}.100\Omega\)
\(U_{cmax}=U\frac{\sqrt{R^2+Z_L^2}}{R}=100\frac{\sqrt{100^2+3.100^2}}{100}=200V\)
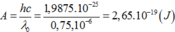
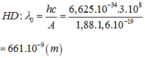

Đáp án A
Giới hạn quang điện được xác định bởi biểu thức