Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Chu kì dao động: T = 2π/ω = 2π/5π = 0,4s
Thời điểm t = 0 và thời điểm độ lớn lực đàn hồi bằng 0,5N được biểu diễn trên đường tròn lượng giác:
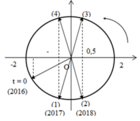
Một chu kì có 4 lần độ lớn lực đàn hồi bằng 0,5N
Sau 504T độ lớn lực đàn hồi bằng 0,5N lần thứ 2016
=> Lực đàn hồi có độ lớn bằng 0,5N lần thứ 2018 vào thời điểm:
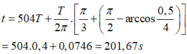

Đáp án D
Phương pháp: Thế năng đàn hồi:
Cách giải:
Độ dãn của lò xo tại vị trí cân bằng: Δ l 0 = m g k = 0,2.10 80 = 0,025 m = 2,5 c m
Biên độ dao động của con lắc: A = 7 , 5 - Δ l 0 = 7 , 5 - 2 , 5 = 5 c m
Ta có: Δ l 0 < A
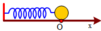
Chọn chiều dương hướng xuống
⇒ Vị trí lực đàn hồi có độ lớn nhỏ nhất là vị trí lò xo không giãn cũng không nén: Δ l = 0
Thế năng đàn hồi tại vị trí đó: W t = 1 2 k Δ l 2 = 1 2 80. ( 0 ) 2 = 0 J

Đáp án A
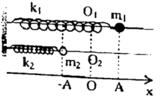
+ Phương trình dao động của hai con lắc lò xo:
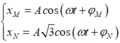
+ Khoảng cách giữa hai vật nặng của hai con lắc lò xo tại thời điểm t là:
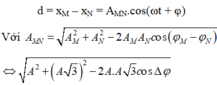
+ Trong quá trình dao động, độ chênh lệch độ cao lớn nhất của hai vật là A:
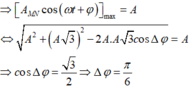
+ Động năng của con lắc M cực đại W dM = kA 2 2 = 0 , 12 J khi vật M ở VTCB. Khi đó ta biểu diễn được vị trí của vật N được biểu diễn trên đường tròn lượng giác (M và N lệch pha nhau góc π/6).
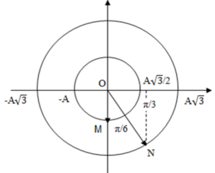
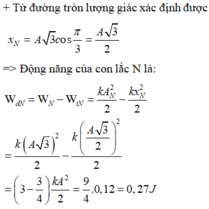

Đáp án A
Phương pháp: Hai vật có cùng li độ khi x 1 = x 2
Cách giải:
Tần số góc của con lắc lò xo 1 và 2:
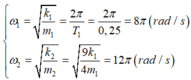
Theo bài ra ta có phương trình dao động của con lắc 1 và 2:

Hai vật có cùng li độ lần thứ 2018 ứng với k = 2018
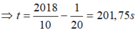

Đáp án A
Phương pháp: Áp dụng định luật bảo toàn cơ năng W = W đ + W t
Cách giải:
Ta có: W = W d + W t ⇒ W d = W − W t = m ω 2 A 2 2 − m ω 2 x 2 2
Khi x = A 2 2 ⇒ W d = m ω 2 A 2 2 − m ω 2 . A 2 2 2 2 = m ω 2 A 2 4
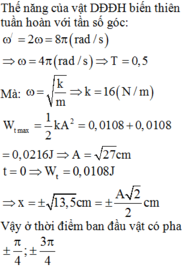
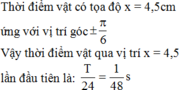

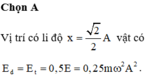

Đáp án D
+ Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác