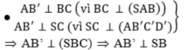Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Ta có: AB vuông góc với BC, SC vuông góc với BC (vì SC vuông góc với mặt đáy ABCD). Vậy AB // SC. Vậy AB vuông góc (SBC).
b/ Tương tự, ta có: AD vuông góc với CD, SC vuông góc với CD. Vậy AD // SC. Vậy AD vuông góc (SCD).
c/ Ta có: SA vuông góc với mặt đáy ABCD (vì S là đỉnh chóp), CI vuông góc với SB (vì đường thẳng CI là hình chiếu của đường thẳng SC lên mặt phẳng chứa SB và CI). Vậy SA // CI. Vậy SA vuông góc CI.
d/ Gọi M là trung điểm của IJ. Ta cần chứng minh SA vuông góc CM. Ta có: CM vuông góc với IJ (vì nằm trên đường trung trực của IJ). Ta cũng có: SA vuông góc CI (đã chứng minh ở câu c). Vậy ta cần chứng minh CI // JM. Từ đó suy ra (SAC) ⊥ (CIJ). Theo tính chất của hình học không gian, ta có CI vuông góc với mặt phẳng (SBC). Tương tự, JI vuông góc với mặt phẳng (SCD). Vậy CI // JI. Điều này suy ra từ tính chất của mặt phẳng và đoạn thẳng vuông góc với mặt phẳng. Suốt đoạn thẳng IJ, ta có thể lấy một điểm nào đó làm trung điểm, ví dụ M. Vậy CI // JM.

a.
\(\Delta_VSAB=\Delta_VSAD\left(c.g.c\right)\Rightarrow AB_1=AD_1\)
\(\Rightarrow SB_1=SD_1\Rightarrow\dfrac{SB_1}{SB}=\dfrac{SD_1}{SD}\)
\(\Rightarrow B_1D_1||BD\) (Talet đảo)
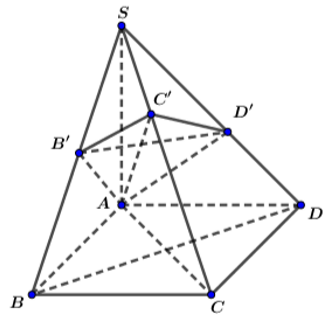
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AB_1\)
\(\Rightarrow AB_1\perp\left(SBC\right)\Rightarrow AB_1\perp SC\)
Hoàn toàn tương tự: \(AD_1\perp\left(SCD\right)\Rightarrow AD_1\perp SC\)
\(\Rightarrow SC\perp\left(AB_1D_1\right)\)
b.
\(\left\{{}\begin{matrix}SC\perp AC_1\\SC\perp\left(AB_1D_1\right)\end{matrix}\right.\) \(\Rightarrow AC_1\in\left(AB_1D_1\right)\)
\(\Rightarrow\) 4 điểm \(A;B_1;C_1;D_1\) đồng phẳng
Theo chứng minh câu a, \(AB_1\perp\left(SBC\right)\Rightarrow AB_1\perp B_1C_1\) (1)
\(AD_1\perp\left(SCD\right)\Rightarrow AD_1\perp\left(D_1C_1\right)\)
\(\Rightarrow B_1;D_1\) cùng nhìn \(AC_1\) dưới 1 góc vuông nên tứ giác \(AB_1C_1D_1\) nội tiếp đường tròn đường kính \(AC_1\)
c.
Gọi E là trung điểm BC
\(\Rightarrow C_1E\) là đường trung bình tam giác SBC
\(\Rightarrow C_1E||SB\Rightarrow\widehat{SB;AC_1}=\widehat{\left(C_1E;AC_1\right)}=\widehat{AC_1E}\)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{3}\)
\(C_1E=\dfrac{1}{2}SB=\dfrac{a\sqrt{3}}{2}\)
\(AE=\sqrt{AB^2+BE^2}=\sqrt{AB^2+\left(\dfrac{BC}{2}\right)^2}=\dfrac{a\sqrt{5}}{2}\)
\(\dfrac{1}{AC_1^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\Rightarrow AC_1=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=a\)
Áp dụng định lý hàm cos cho tam giác \(AEC_1\):
\(cos\widehat{AC_1E}=\dfrac{AC_1^2+C_1E^2-AE^2}{2AC_1.C_1E}=0\Rightarrow\widehat{AC_1E}=90^0\)