NT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
5
LM
4 tháng 2 2016
Xét ( a2 + b2 + c2 + d2 ) - ( a + b + c + d)
= a(a -1) + b( b -1) + c( c – 1) + d( d – 1)
Vì a là số nguyên dương nên a, (a – 1) là hai số tự nhiên liên tiếp
=> a(a-1) chia hết cho 2. Tương tự ta có b(b-1); c(c-1); d(d-1) đều chia hết cho 2
=> a(a -1) + b( b -1) + c( c – 1) + d( d – 1) là số chẵn
Lại có a2 + c2 = b2 + d2=> a2 + b2 + c2 + d2 = 2( b2 + d2) là số chẵn.
Do đó a + b + c + d là số chẵn mà a + b + c + d > 2 (Do a, b, c, d thuộc N*)
a + b + c + d là hợp số.
19 tháng 4 2018
Xét \(( a^2 + b^2 + c^2 + d^2 ) - ( a + b + c + d)\)
\(= a(a -1) + b( b -1) + c( c – 1) + d( d – 1)\)
Vì a là số nguyên dương nên $a$, $(a – 1)$ là hai số tự nhiên liên tiếp
\(\Rightarrow a-1⋮2\)
Tương tự ta có $b(b-1)$; $c(c-1)$; $d(d-1)$ đều chia hết cho 2
=> $a(a -1) + b( b -1) + c( c – 1) + d( d – 1)$ là số chẵn
Lại có \(a^2 + c^2 = b^2 + d^2=> a^2 + b^2 + c^2 + d^2 = 2( b^2 + d^2)\) là số chẵn.
Do đó $a + b + c + d$ là số chẵn mà $a + b + c + d > 2$ (Do \(a,b,c,d\in N^{sao}\))
\(\Rightarrow\) $a + b + c + d$ là hợp số.
17 tháng 6 2019
15.
Ta có \(a+b+c+ab+bc+ac=6\)
Mà \(ab+bc+ac\le\left(a+b+c\right)^2\)
=> \(\left(a+b+c\right)^2+\left(a+b+c\right)-6\ge0\)
=> \(a+b+c\ge3\)
\(A=\frac{a^4}{ab}+\frac{b^4}{bc}+\frac{c^4}{ac}\ge\frac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ac}\ge a^2+b^2+c^2\ge\frac{1}{3}\left(a+b+c\right)^2\ge3\)(ĐPCM)
17 tháng 6 2019
Bài 18, Đặt \(\left(a^2-bc;b^2-ca;c^2-ab\right)\rightarrow\left(x;y;z\right)\) thì bđt trở thành
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow x^3+y^3+z^3-3xyz\ge0\)
\(\Leftrightarrow\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\ge0\)
\(\Leftrightarrow\frac{1}{2}\left(x+y+z\right)\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]\ge0\)
Vì \(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)nên ta đi chứng minh \(x+y+z\ge0\)
Thật vậy \(x+y+z=a^2-bc+b^2-ca+c^2-ab\)
\(=\frac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\ge0\)(đúng)
Tóm lại bđt được chứng minh
Dấu "=": tại a=b=c
27 tháng 1 2016
BÀI TOÁN PHỤ: CHứng minh rằng số chính phương lẻ chia cho 8 dư 1.
Giải: Xét số chính phương lẻ là \(m^2\left(m\in Z\right)\)
Như vậy m là số lẻ, đặt \(m=2n+1\)
Ta có:
\(m^2=\left(2n+1\right)^2=4n^2+4n+1=4.n.\left(n+1\right)+1\)
Vì n(n+1) là tích 2 số nguyên liên tiếp nên chia hết cho 2
\(\Rightarrow4n\left(n+1\right) \) chia hết cho 8
\(\Rightarrow4.n.\left(n+1\right)+1\) chia 8 dư 1
Vậy ta có điều phải chứng minh.
Vì a lẻ nên \(a\ne0\), phương trình \(ax^2+bx+c=0\) là phương trình bậc hai.
Xét \(\Delta=b^2-4ac\): b lẻ, theo bài toán phụ có \(b^2=8k+1\left(k\in Z\right)\)
a,c lẻ \(\Rightarrow\) \(ac\) lẻ
Đặt \(ac=2l-1\left(l\in Z\right)\)
Do đó \(\Delta=b^2-4ac=8k+1-4.\left(2l-1\right)=8k+1-8l+4=8\left(k-l\right)+5 \)chia cho 8 dư 5, theo bài toán phụ trên ta có \(\Delta\) không phải số chính phương.
\(\Delta\) là số nguyên, không phải óố chính phương \(\Rightarrow\sqrt{\Delta}\) là số vô tỉ
Nghiệm của phương trình đã cho (nếu có) là: \(x=\frac{-b\pm\sqrt{\Delta}}{2a}\)
b,a\(\in Z\), \(\sqrt{\Delta}\) vô tỉ nên x là vô tỉ.
Vậy phương trình có nghiệm nếu có thì các nghiệm ấy không thể là số hữu tỉ.
ơng là phươngax2+bx+c=0
AH
Akai Haruma
Giáo viên
29 tháng 12 2016
Lời giải:
Từ điều kiện đề bài dễ dàng suy ra \(a,b,c<\sqrt{3}<2\)
Sử dụng phương pháp hệ số bất định, ta sẽ CM: \(2a+\frac{1}{a}\geq \frac{5}{2}+\frac{a^2}{2}\)
BĐT này luôn đúng vì \(\Leftrightarrow (2-a)(a-1)^2\geq 0\)
Thiết lập tương tự với $b,c$, suy ra \(2(a+b+c)+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq \frac{15}{2}+\frac{a^2+b^2+c^2}{2}=9\) (đpcm)
Dấu $=$ xảy ra khi $a=b=c=1$
và 
.
CM
16 tháng 7 2019
Đáp án C.
Ta có
log b a 2018 = log b a 2018 ⇔ log b a 2018 = 2018 log b a ⇔ log b a = 0 log b a 2017 = 2018
⇔ a = 1 log b a = 2018 2017 ⇔ a = 1 a = b 2018 2017
Do a là số thực dương nên với mỗi số nguyên b thỏa mãn điều kiện 2 ≤ b ≤ 200 thì sẽ tạo ra một cặp số a ; b thỏa mãn yêu cầu đề bài.
Do vậy có 2 × 200 − 2 1 + 1 = 398 cặp. Vậy ta chọn C.
Lời giải sai: log b a 2018 = 2018 log b a ⇔ log b a 2017 = 2018 , tức là bỏ mất trường hợp log b a = 0 , từ đó dẫn đến chọn đáp án B
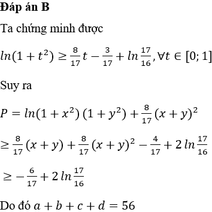
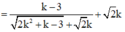
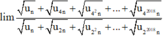
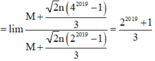ko có