Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Xét đạo hàm sau:
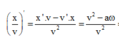
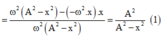
+ Xét biểu thức x 1 v 1 + x 2 v 2 = x 3 v 3
+ Lấy đạo hàm hai vế và áp dụng đạo hàm (1) ta có:
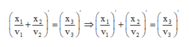
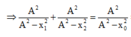
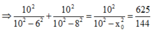
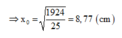

Đáp án C
Phương pháp: 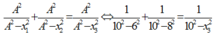
Cách giải:
Ta có: 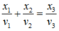
Đạo hàm hai vế của phương trình theo t ta được:
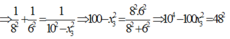
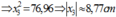

+ Xét đạo hàm sau:
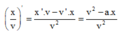
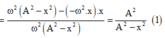
+ Xét biểu thức: x 1 v 1 + x 2 v 2 = x 3 v 3
+ Lấy đạo hàm hai vế và áp dụng đạo hàm (1) ta có:
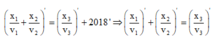
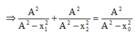
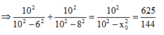
⇒ x 0 = 1924 25 = 8 , 77 ( c m )

Đáp án C
Phương pháp: Sử dụng công thức độc lập với thời gian kết hợp với đạo hàm
Cách giải:
Theo đề bài ta có
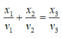
, đạo hàm hai vế của phương trình trên ta được:
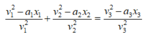
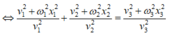
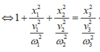
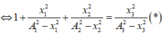
Theo đề bài cho
![]()
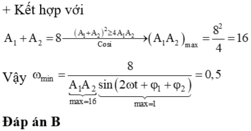
tại thời điểm t ta có:
![]()
Thay vào biểu thức (*) ta tính được x 0 = x 3 = 6 , 4 c m
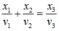

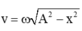
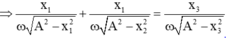
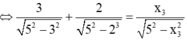
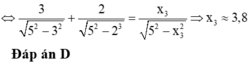

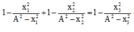
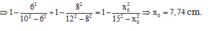

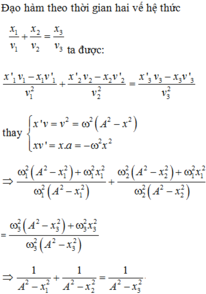
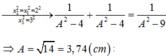
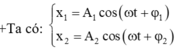
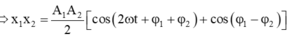
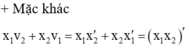
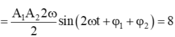
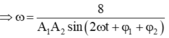
Ta có: \(\left(\frac{v}{x}\right)'=\frac{v^2-ax}{v^2}\)
Mà: \(a=-\omega^2x\) nên \(\left(\frac{v}{x}\right)'=1+\frac{\omega^2x}{v^2}=1+\frac{x^2}{\frac{v^2}{\omega^2}}=1+\frac{x^2}{A^2-x^2}\)
Đạo hàm 2 vế biểu thức đã cho ta có:
\(1+\frac{x_1^2}{A^2-x_1^2}+1+\frac{x_2^2}{A^2-x_2^2}=1+\frac{x_3^2}{A^2-x_3^2}\)
Thay số vào ta tìm đc giá trị \(x_0\)
Em hiểu thế này có đúng không ạ? Tại em biến đổi phương trình đầu tiên của nhưng mà không có ra?
\((\frac{x}{v})' = \frac{x'.v - v'.x}{v^2}= \frac{v^2-ax}{v^2}\)
hay là
\((\frac{v}{x})'= \frac{ax - x^2}{v^2}\)