Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(f\left(x\right)=ax^{3\:}+bx^2+cx+d\left(a\ne0\right)\)
Nếu \(a< 0\) thì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\\\lim\limits_{x\rightarrow+\infty}f\left(x\right)=-\infty\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)\in\left(-\infty;+\infty\right)\), với \(x\in\left(-\infty;+\infty\right)\)
\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm
Nếu \(a>0\) thì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-\infty\\\lim\limits_{x\rightarrow+\infty}f\left(x\right)=+\infty\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm

Chọn B
Số phần tử của tập hợp E là ![]()
Vì ![]()
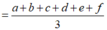
![]()
Mà chia hết cho 3 nên khi lấy ra 6 chữ số thỏa điều kiện ta phải loại ra một số chia hết cho 3. Ta có 3 trường hợp sau:
1) Trường hợp 1:
Loại bỏ số 0, khi đó a + b = c + d = e + f = 7
Bước 1: Chia ra làm 3 cặp số có tổng bằng 7 là : (1;6), (2;5), (3;4) có 1 cách chia.
Bước 2: Chọn a có 6 cách; chọn b có 1 cách; chọn c có 4 cách; chọn d có 1 cách; chọn e có 2 cách; chọn f có 1 cách: có 6.1.4.1.2.1 = 48 cách.
Trường hợp này có 48 số.
2) Trường hợp 2:
Loại bỏ số 3, khi đó a + b = c + d = e + f = 6
Bước 1: Chia ra làm 3 cặp số có tổng bằng 6 là : (0;6), (1;5), (2;4) có 1 cách chia.
Bước 2: Chọn a có 5 cách (vì có số 0); chọn b có 1 cách; chọn c có 4 cách; chọn d có 1 cách; chọn e có 2 cách; chọn f có 1 cách: có 5.1.4.1.2.1 = 40 cách.
Trường hợp này có 40 số.
3) Trường hợp 3:
Loại bỏ số 6, khi đó a + b = c + d = e + f = 5. Tương tự như trường hợp 2, có 40 số.
Vậy trong tập hợp E có tất cả 48 + 40 + 40 = 128 số có dạng a b c d e f ¯ sao cho a + b = c + d = e + f
Xác suất cần tìm là: ![]()

\(f'\left(x\right)=2ax+b\)
\(f\left(x\right)+\left(x-1\right)f'\left(x\right)=ax^2+bx+c+\left(x-1\right)\left(2ax+b\right)\)
\(=3ax^2+\left(2b-2a\right)x+c-b\)
Yêu cầu bài toán thỏa mãn khi: \(\left\{{}\begin{matrix}3a=3\\2b-2a=0\\c-b=0\end{matrix}\right.\) \(\Leftrightarrow a=b=c=1\)

\(\left(c;d\right)\Rightarrow\left(-c;-d\right)\)
\(\left(a-1\right)^2+\left(b-1\right)^2=1\)
\(\left(c-5\right)^2+\left(d-5\right)^2=100\)
Gọi \(A\left(a;b\right)\) thuộc đường tròn có pt \(\left(x-1\right)^2+\left(y-1\right)^2=1\) (C) có tâm \(I\left(1;1\right)\) bán kính \(R=1\)
\(B\left(d;c\right)\) thuộc đường tròn có pt \(\left(x-5\right)^2+\left(y-5\right)^2=100\) (C') có tâm \(I'\left(5;5\right)\) bán kính \(R=10\)
\(\Rightarrow AB^2=P=\left(a-d\right)^2+\left(b-c\right)^2\)
\(P_{min}\Leftrightarrow A;B\) là giao điểm nằm cùng phía so với I và I' của đường thẳng II' với 2 đường tròn
Phương trình II': \(x-y=0\)
\(\Rightarrow A\left(\dfrac{2-\sqrt{2}}{2};\dfrac{2-\sqrt{2}}{2}\right)\) ; \(B\left(5-5\sqrt{2};5-5\sqrt{2}\right)\)
\(\Rightarrow P_{min}=AB=\dfrac{9\sqrt{2}-8}{\sqrt{2}}=9-4\sqrt{2}\)


Dùng xích ma á
S=55252
???