Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Số a không thể bằng 0 do đó a , b , c ∈ 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6
Với mỗi cách chọn ra 3 số bất kì trong tập 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ta được 1 số thỏa mãn a < b < c
Do đó C 6 3 = 20 số

Chọn B
Số phần tử của tập hợp E là ![]()
Vì ![]()
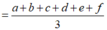
![]()
Mà chia hết cho 3 nên khi lấy ra 6 chữ số thỏa điều kiện ta phải loại ra một số chia hết cho 3. Ta có 3 trường hợp sau:
1) Trường hợp 1:
Loại bỏ số 0, khi đó a + b = c + d = e + f = 7
Bước 1: Chia ra làm 3 cặp số có tổng bằng 7 là : (1;6), (2;5), (3;4) có 1 cách chia.
Bước 2: Chọn a có 6 cách; chọn b có 1 cách; chọn c có 4 cách; chọn d có 1 cách; chọn e có 2 cách; chọn f có 1 cách: có 6.1.4.1.2.1 = 48 cách.
Trường hợp này có 48 số.
2) Trường hợp 2:
Loại bỏ số 3, khi đó a + b = c + d = e + f = 6
Bước 1: Chia ra làm 3 cặp số có tổng bằng 6 là : (0;6), (1;5), (2;4) có 1 cách chia.
Bước 2: Chọn a có 5 cách (vì có số 0); chọn b có 1 cách; chọn c có 4 cách; chọn d có 1 cách; chọn e có 2 cách; chọn f có 1 cách: có 5.1.4.1.2.1 = 40 cách.
Trường hợp này có 40 số.
3) Trường hợp 3:
Loại bỏ số 6, khi đó a + b = c + d = e + f = 5. Tương tự như trường hợp 2, có 40 số.
Vậy trong tập hợp E có tất cả 48 + 40 + 40 = 128 số có dạng a b c d e f ¯ sao cho a + b = c + d = e + f
Xác suất cần tìm là: ![]()

a. Có 4 cách chọn chữ số hàng đơn vị
6 cách chọn chữ số hàng nghìn
7 cách chọn chữ số hàng trăm
7 cách chọn chữ số hàng chục
⇒ Theo quy tắc nhân: Có 4.6.7.7 = 1176 (số)
b. TH1: Chọn các số chẵn có chữ số hàng đơn vị bằng 0
⇒ Có 6 cách chọn chữ số hàng nghìn
5 cách chọn chữ số hàng trăm
4 cách chọn chữ số hàng chục
⇒ Theo quy tắc nhân: có 6.5.4 = 120 (số)
TH2: Chọn các số chẵn có chữ số hàng đơn vị khác 0.
⇒ Có 3 cách chọn chữ số hàng đơn vị
Có 5 cách chọn chữ số hàng nghìn (khác 0 và khác hàng đơn vị)
Có 5 cách chọn chữ số hàng trăm
Có 4 cách chọn chữ số hàng chục
⇒ Theo quy tắc nhân: Có 3.5.5.4 = 300 (số)
⇒ Theo quy tắc cộng: Có tất cả 120 + 300 = 420 số chẵn thỏa mãn.

Đáp án B
TH1: 4 chữ số a, b, c , d khác nhau → có C 9 4 số
TH2: Trong 4 chữ số a, b, c , d có 3 chữ số giống nhau → có 3 C 9 3 số
TH3: Trong 4 chữ số a, b, c , d có 2 chữ số giống nhau → có 2 C 9 1 số
TH4: TH1: 4 chữ số a, b, c , d giống nhau → có C 9 1 số
Vậy có tất cả C 9 4 + 3 C 9 3 + 2 C 9 1 + C 9 1 = 459 số cần tìm.

Đáp án B
Phương pháp: Vì số cần lập có a < b < c và a ≠ 0 nên a = 1 ; 2 ; 3 ; 4 . Như vậy ta xét các TH sẽ tìm được số các chữ số cần lập.
Cách giải: Các số được lập thỏa mãn a < b < c.. Khi đó ta có các trường hợp sau:
TH1: Với a = 1 thì b ∈ 5 ; 4 ; 3 ; 2
+) a = 1; b = 2 => c có 4 cách chọn => có 1.1.4 = 4 số
+) a = 1; b = 3 => c có 3 cách chọn => có 1.1.3 = 3 số.
+) a = 1; b = 4 => c có 2 cách chọn => có 1.1.2 = 2 số.
+) a = 1; b = 5 => có 1 cách chọn => có 1.1.1 = 1 số.
Như vậy TH này có: 4 + 3 + 2 + 1 = 10 số được chọn.
TH2: Với a = 2 thì b ∈ 5 ; 4 ; 3
+) a = 2; b = 3 => có 3 cách chọn => có 1.1.3 = 3 số.
+) a = 2; b = 4 => c có 2 cách chọn => có 1.1.2 = 2 số.
+) a = 2; b = 5 => c có 1 cách chọn => có 1.1.1 = 1 số.
Như vậy TH này có: 3 + 2 + 1 = 6 số được chọn.
TH3: Với a = 3 thì b ∈ 4 ; 5
+) a = 3; b = 4 => c có 2 cách chọn => có 1.1.2 = 2 số.
+) a = 3; b = 4 => c có 1 cách chọn => có 1.1.1 = 1 số.
Như vậy TH này có: 2 + 1 = 3 số được chọn.
TH4: Với a = 4 thì b = 5 ta có các số được chọn: 456 hay có 1 số được chọn.
Như vậy có tất cả: 10 + 6 + 3 + 1 = 20 số được chọn.