Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Ta có:
g ' x = 2 x − 8 f ' x 2 − 8 x + m = 0 ⇔ x = 4 f ' x 2 − 8 x + m = 0 ( * ) .
Mà:
f ' x = x − 1 2 x 2 − 2 x = x − 1 2 . x x − 2 ; ∀ x ∈ ℝ .
Suy ra (*)
⇔ x 2 − 8 x + m − 1 2 x 2 − 8 x + m x 2 − 8 x + m − 2 = 0 ⇔ x 2 − 8 x + m − 1 = 0 1 x 2 − 8 x + m = 0 2 x 2 − 8 x + m − 2 = 0 3
Để hàm số đã cho có 5 điểm cực trị khi và chỉ khi:
TH1. (1) có nghiệm kép x = 4 , (2), (3) có 2 nghiệm phân biệt.
TH2. (1) không có nghiệm kép x = 4 , (2), (3) có 2 nghiệm phân biệt.
Khi đó m < 16 là các giá trị thỏa mãn. Kết hợp m ∈ ℤ + ⇒ có 15 giá trị m cần tìm.
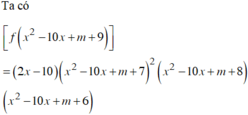


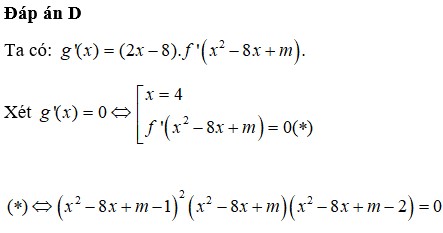
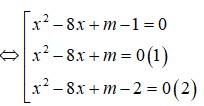


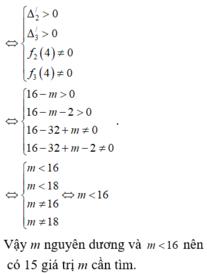
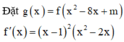



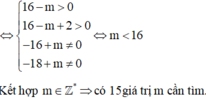
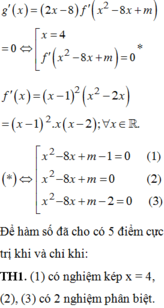


Đáp án B
y = 3 x 4 − 4 x 3 − 12 x 2 + m = f ( x ) + m , ( f ( x ) = 3 x 4 − 4 x 3 − 12 x 2 ) f ' ( x ) = 12 x 3 − 12 x 2 − 24 x = 12 x ( x + 1 ) ( x − 2 ) y ' = f ' ( x ) ( f ( x ) + m ) f ( x ) + m = 0 ⇒ f ' ( x ) = 0 f ( x ) = − m
Dựa vào BBT ta thấy hàm số có 5 điểm cực trị khi và chỉ khi
− m > 0 − 32 < − m ≤ − 5 ⇒ m < 0 5 ≤ m < 32 ⇒ m = 5 ; 6 ; ...31