Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Có \(C_6^3\) cách chọn 3 nam từ 6 nam
b.
Chọn 2 nam từ 6 nam và 3 nữ từ 9 nữ để lập tổ 1 có: \(C_6^2.C_9^3\) cách
Chọn 2 nam từ 4 nam còn lại và 3 nữ từ 6 nữ còn lại để lập tổ 2 có: \(C_4^2.C_6^3\) cách
Chọn 2 nam từ 2 nan còn lại và 3 nữ từ 3 nữ còn lại: \(C_2^2.C_3^3\) cách
\(\Rightarrow C_6^2.C_9^3+C_4^2.C_6^3+C_2^2.C_3^3\) cách thỏa mãn chia 3 tổ

Chọn D
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố: “cặp sinh đôi ngồi cạnh nhau và nam nữ không ngồi đối diện nhau”.
Ta tính n() như sau:
Đánh số các ghế ngồi của 8 học sinh như hình vẽ sau:
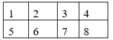
- Để xếp cho cặp sinh đôi ngồi cạnh nhau có 6 cách.
- Mỗi cách như vậy có cách đổi chỗ.
- Với mỗi cách xếp cặp sinh đôi, ví dụ: Cặp sinh đôi ở vị trí 1 và 2.
Do nam nữ không ngồi đối diện nên:
+ Vị trí 5 và 6 đều có 3 cách.
+ Vị trí 3 có 4 cách, vị trí 7 có 1 cách.
+ Vị trí 4 có 2 cách, vị trí 8 có 1 cách.
Suy ra n(A) = 6.2.3.3.4.1.2.1 = 864
![]()

Bạn ơi mình nghĩ bài này phải chia trường hợp ra
VD : TH1: xếp vào tổ 1 : 2 hsg, 2 học sinh khá và 4 học sinh TB thì sẽ có \(C_3^2.C^2_5.C^4_8\) cách chọn
Tương tự các trường hợp còn lại
Mọi người góp ý giúp mình nha
Do ko phân biệt hai tổ (ko cần hoán vị) nên chỉ cần xếp cho 1 tổ, tổ còn lại là phần còn lại (luôn thỏa mãn khi phần 1 thỏa mãn)
Giả sử ta xếp vào tổ có 2 học sinh giỏi \(\Rightarrow C_3^2=3\) cách chọn (1 hsg kết quả cũng vậy)
- Nếu xếp vào 2 hs khá \(\Rightarrow C_5^2=10\) cách chọn
Còn lại 4 bạn trung bình \(\Rightarrow C_8^4=70\)
\(\Rightarrow700\) cách xếp
- Nếu xếp vào 3 hs khá: \(\Rightarrow C_5^3=10\) cách
Còn 3 bạn trung bình: có \(C_8^3=56\) cách
\(\Rightarrow560\) cách
Tổng cộng có: \(3\left(700+560\right)=3780\) cách


Số cách phân nhóm 5 học sinh trong số 8 học sinh là C 8 5 . Sau khi phân nhóm 5 học sinh còn lại 3 học sinh được phân hóm còn lại. Vậy sẽ có C 8 5 cách
Chọn B