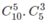Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chọn 7 người từ 10 để lập một nhóm, ba người còn lại vào nhóm khác. Vậy số cách chia là \(C^7_{10}\)
b) Tương tự, kết quả là \(C^5_{10}.C^3_5\)

Khi chọn 1 nhóm thì nhóm kia hoàn toàn xác định (vì là những người còn lại).
Sậy số cách chia hai nhóm bằng số cách chọn ra 1 nhóm có 9 người hoặc 10 người, trong đó có 5 hoặc 6 nữ.
Ta có:
-Số cách chọn 10 người, trong đó có 5 nữ bằng số cách chọn 5 nam từ 8 nam và 5 nữ từ 11 nữ và bằng \(C_8^5.C_{11}^5\)
-Số cách chọn 9 người, trong đó có 5 nữ bằng số cách chọn 4 nam từ 8 nam và 5 nữ từ 11 nữ và bằng \(C_8^4.C_{11}^5\)
-Số cách chọn 10 người, trong đó có 6 nữ bằng số cách chọn 4 nam từ 8 nam và 6 nữ từ 11 nữ và bằng \(C_8^4.C_{11}^6\)
-Số cách chọn 9 người, trong đó có 6 nữ bằng số cách chọn 3 nam từ 8 nam và 6 nữ từ 11 nữ và bằng \(C_8^3.C_{11}^6\)
Tổng số cách chọn là: \(C_8^5.C_{11}^5\)+ \(C_8^4.C_{11}^5\)+ \(C_8^4.C_{11}^6\) + \(C_8^3.C_{11}^6\)

Đáp án D
Xem lô đất có 4 vị trí gồm 2 vị trí 1 nền,1 vị trí 2 nền và 1 vị trí 3 nền
Bước 1: nhóm thứ nhất chọn 1 vị trí cho 2 nền có 4 cách và mỗi cách có 2!=2 cách chọn nền cho mỗi người.
Suy ra có 4.2=8 cách chọn nền
Bước 2 nhóm thứ hai chọn 1 trong 3 vị trí còn lại cho 3 nền có 3 cách và mỗi cách có 3!=6 cách chọn nền cho mỗi người.
Suy ra có 3.6=18 cách chọn nền
Vậy có 8.18=144 cách chọn nền cho mỗi người

Xem lô đất có 4 vị trí gồm 2 vị trí 1 nền, 1 vị trí 2 nền và 1 vị trí 3 nền.
Bước 1: nhóm thứ nhất chọn 1 vị trí cho 2 nền có 4 cách và mỗi cách có 2!=2 cách chọn nền cho mỗi người. Suy ra có 4.2 = 8 cách chọn nền.
Bước 2: nhóm thứ hai chọn 1 trong 3 vị trí còn lại cho 3 nền có 3 cách và mỗi cách có 3!= 6 cách chọn nền cho mỗi người.
Suy ra có 3.6=18 cách chọn nền.
Vậy có 8.18=144 cách chọn nền cho mỗi người
Chọn A.

a: Coi 3 bạn nữ như 1 người
Số cách xếp là:
\(8!\cdot3!\)(cách)
b: Số cách xếp là:
\(10!-8!\cdot3!\left(cách\right)\)

Số cách phân nhóm 5 học sinh trong số 8 học sinh là C 8 5 . Sau khi phân nhóm 5 học sinh còn lại 3 học sinh được phân hóm còn lại. Vậy sẽ có C 8 5 cách
Chọn B

ta có các TH xảy ra :
TH1: 3 nữ và 5 nam=> ta có \(C^3_5.C^5_{10}=2520\) cách
TH2: 4 nam và 4 nữ=> có : \(C^4_5.C^4_{10}=1050\)cách
TH3:5nam và 3 nữ: => có: \(C^5_5.C^3_{10}=120\)cách
=.> có tất cả 3690 cách

a) Chọn 7 người từ 10 người để lập một nhóm, ba người còn lại vào nhóm khác. Vậy số cách chia là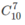
b) Ba nhóm tương ứng gồm 5, 3, 2 người, sẽ có số cách chia là