Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Do x 1 v à x 2 vuông pha nên x 1 A 1 2 + x 2 A 2 2 = 1
Tương tự x 2 v à x 3 vuông pha nên: x 2 A 2 2 + x 3 A 3 2 = 1
Tại thời điểm t 2 : - 20 A 1 2 + 0 A 2 2 = 1 ⇒ A 1 = 20 c m
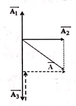
Tại thời điểm t 1
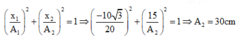
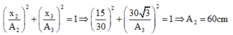
Từ giản đồ Frenel (hình vẽ) ta có: A = A 2 2 + ( A 3 - A 1 2 ) = 50 c m

Đáp án D
+ Biên độ dao động tổng hợp có giá trị nằm trong khoảng A 1 − A 2 ≤ A ≤ A 1 + A 2 → 7 cm ≤ A ≤ 23 cm.
→ A không thể là 6 cm.

+ Phương pháp giản đồ vecto
+ Từ hình vẽ, ta thấy rằng A2 ≤ OH.
Áp dụng hệ thức lượng trong tam giác, ta thu được


Đáp án A


+ Do x1 và x2 vuông pha nên: x 1 A 1 2 + x 2 A 2 2 = 1
+ Tương tự x2 và x3 vuông pha: x 2 A 2 2 + x 3 A 3 2 = 1
+ Tại thời điểm t 2 : − 20 A 1 2 + 0 A 2 2 = 1 ⇒ A 1 = 20 c m
+ Tại thời điểm t 1 : x 1 A 1 2 + x 2 A 2 2 = 1 ⇒ − 10 3 20 2 + 15 A 2 2 = 1 ⇒ A 2 = 30 c m
x 2 A 2 2 + x 3 A 3 2 = 1 ⇒ 15 30 2 + 30 3 A 1 2 = 1 ⇒ A 3 = 60 c m
+ Từ giản đồ: A = A 2 2 + A 3 − A 1 2 = 50 c m
Chọn đáp án A

Đáp án D
Phương pháp: Sử dụng điều kiện về biên độ của dao động tổng hợp trong bài toán tổng hợp hai dao động điều hòa
Cách giải :
Ta có
![]()
Do đó biên độ không thể nhận giá trị 32 cm

Đáp án B
HD: Biên độ dao động tổng hợp có giá trị nằm trong khoảng:


Chọn đáp án B
Nhận thấy x 1 và x 3 ngược pha nhau và cùng vuông pha với x 2 nen tại thời điểm t 2 thì x 2 = 0 nên
x 1 = − 20 c m = − A 1 ; x 3 = 60 c m = A 3
Mặt khác x 1 vuông pha x 2 nên tại thời điểm t 1 ta có:
− 10. 3 2 20 2 + 15 2 A 2 2 = 1 ⇒ A 2 = 30 .
Biên độ dao động tổng hợp:
A = A 1 − A 3 2 + A 2 2 = 40 2 + 30 2 = 50 c m
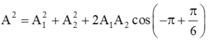
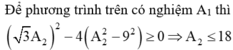


$x_1$ vuông pha với $x_2$ $\Rightarrow $$x_{12}$=$\sqrt{16^2+A_2^2}$
Đề không tồn tại sự tổng hợp dao động này thì $A_{123}$ max < 25cm
$\Rightarrow $ $16^2$+$A_2^2$+25+2.5.$\sqrt{16^2+A_2^2}$ < $25^2$
$\sqrt{16^2+A_2^2}$<20$\Rightarrow $ $A_2$ < 12
Chọn B.