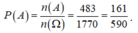Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số cách rút sao cho có 1 số chia hết cho 10:
\(C_6^1.C_{54}^1=324\) cách
Số cách rút sao cho 1 số chia hết cho 5, một số là số chẵn và không số nào trong chúng chia hết cho 10:
\(C_6^1.C_{24}^1=144\) cách
Xác suất: \(P=\frac{324+144}{C_{60}^2}=\frac{78}{295}\)

Xác suất lấy ra quả cầu không có số 1 hoặc số 5 từ túi đầu tiên: \(\frac{8}{{10}} = \frac{4}{5}\)
Xác suất lấy được quả cầu không có số 1 hoặc số 5 từ túi thứ hai là: \(\frac{8}{{10}} = \frac{4}{5}\)
Vì lấy ngẫu nhiên từ hai túi khác nhau một quả cầu nên hai biến cố quả cầu lấy ra mỗi túi không có số 1 hoặc số 5 là độc lập.
Vậy xác suất để trong hai quả cầu được lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5 là: \(\frac{4}{5}.\frac{4}{5} = \frac{{16}}{{25}}\)

\(n\left(\Omega\right)=C^3_{30}=4060\)
n(A)\(C^1_{15}\cdot C^2_{15}=1575\)
=>P=1575/4060=45/116

Đáp án B
Lấy ngẫu nhiên 1 quả cầu trong 9 quả cầu có
![]()
Gọi A là biến cố “ lấy được quả cầu được đánh số là chẳn”
Trong 9 quả cầu đánh số, có các số chẵn là 2; 4; 6; 8
suy ra n(A) = 4
Vậy P ( A ) = 4 9

Không gian mẫu: \(C_{15}^3=455\)
Số cách chọn 3 quả sao cho vừa khác màu vừa khác số:
\(4.4.4=64\)
Xác suất: \(P=\dfrac{64}{455}\)

Rõ ràng trong hộp có 30 quả với 15 quả ghi số chẵn, 10 quả màu đỏ, 5 quả màu đỏ ghi số chẵn, 25 quả màu xanh hoặc ghi số lẻ. Vậy theo định nghĩa
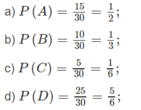
Trong đó A, B, C, D là các biến cố tương ứng với các câu a), b), c) ,d).

Chọn D
Chọn ngẫu nhiên một quả trong 30 quả có 30 cách. Vậy n ( Ω ) = 30.
Gọi A là biến cố: “lấy được quả cầu màu xanh”.
Ta có n(A) = 20 => P(A) = 2 3
Gọi B là biến cố: “lấy được quả cầu ghi số lẻ”.
Ta có n(B) = 15 => P(B) = 1 2 .
Số quả cầu vừa màu xanh vừa ghi số lẻ: 10 (quả).
Xác suất để lấy được quả cầu vừa màu xanh vừa ghi số lẻ: 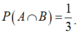
Xác suất để lấy được quả cầu màu xanh hay ghi số lẻ:
![]()
![]()

- Số cách lấy ngẫu nhiên 2 quả cầu: \(n\left( \Omega \right) = C_9^2 = 36\)
- Số cách lấy 2 quả khác màu là:
+ 1 quả màu xanh và 1 quả màu vàng: \(C_4^1 \times C_3^1 = 12\)
+ 1 quả màu xanh và 1 quả màu đỏ: \(C_4^1 \times C_2^1 = 8\)
+ 1 quả màu đỏ và 1 quả màu vàng: \(C_2^1 \times C_3^1 = 6\)
=> Tổng số cách lấy ra 2 quả khác màu là: 26 cách
- Số cách lấy 2 quả khác màu trùng số:
+ 2 quả cùng là số 1: \(C_3^2 = 3\)
+ 2 quả cùng là số 2: \(C_3^2 = 3\)
+ 2 quả cùng là số 3: \(C_2^2 = 1\)
=> Tổng số cách lấy ra 2 quả khác màu trùng số là: 7 cách
=> Số cách lấy ra 2 quả khác màu khác số là: 26 – 7 = 19 (cách)
=> Xác suất để lấy ra 2 quả khác màu khác số là: \(P = \frac{{19}}{{36}}\)
Chọn B
Số phần tử của không gian mẫu là: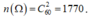 .
.
Gọi A: “ Biến cố lấy đồng thời ngẫu nhiên hai quả cầu sao cho tích của các số trên hai quả cầu chia hết cho 10”.
TH1: Hai quả cầu bốc được có chữ số tận cùng là 0 có C 6 2 (cách).
TH2: Hai quả cầu bốc được có 1 quả cầu có chữ số tận cùng là 0 có (cách).
(cách).
TH3: Hai quả cầu bốc được có 1 quả cầu có chữ số tận cùng là 5 và 1 quả cầu có chữ số tận cùng là 2,3,6,8 có
Khi đó số phần tử của biến cố A là .
.
Vậy xác suất của biến cố A là: