DT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 6 2015
Xét nhà toán học A bất kì nào đó, ông viết thư cho 16 nhà toán học còn lại để trao đổi về ba vấn đề. Theo nguyên lý Đi-rich-lê:ông phải trao đổi một vấn đề nào đó ít nhất với 6 người.Gọi vấn đề đó là vấn đề 1.
Có một nhóm 6 người cùng trao đổi vấn đề 1 với giáo sư A. Nếu trông số họ có 2 người cũng trao đổi về vấn đề 1 thì bài toán được giải quyết.
Nếu không, 6 người đó chỉ trao đổi về hai vấn đề còn lại. Xét nhà toán học B trong số họ. Ông trao đổi với 5 người còn lại trong nhóm về hai vấn đề. Theo nguyên lí Đi-rích-lê: phải có một vấn đề ông trao đổi với ít nhất 3 người bạn.Gọi vấn đề đó là 2. Ta có nhóm 3 người cùng trao đổi với nhà toán học B về vấn đề 2, và không trao đổi với nhau về vấn đề 1.
Nếu trong họ có 2 người trao đổi với nhau vấn đề 2. Bài toán được giải quyết.
Nếu không 3 người họ chỉ trao đổi với nhau về vấn đề 3
MT
4 tháng 6 2015
Xét nhà toán học A bất kì nào đó, ông viết thư cho 16 nhà toán học còn lại để trao đổi về ba vấn đề. Theo nguyên lý Đi-rich-lê:ông phải trao đổi một vấn đề nào đó ít nhất với 6 người.Gọi vấn đề đó là vấn đề 1.
Có một nhóm 6 người cùng trao đổi vấn đề 1 với giáo sư A. Nếu trông số họ có 2 người cũng trao đổi về vấn đề 1 thì bài toán được giải quyết.
Nếu không, 6 người đó chỉ trao đổi về hai vấn đề còn lại. Xét nhà toán học B trong số họ. Ông trao đổi với 5 người còn lại trong nhóm về hai vấn đề. Theo nguyên lí Đi-rích-lê: phải có một vấn đề ông trao đổi với ít nhất 3 người bạn.Gọi vấn đề đó là 2. Ta có nhóm 3 người cùng trao đổi với nhà toán học B về vấn đề 2, và không trao đổi với nhau về vấn đề 1.
Nếu trong họ có 2 người trao đổi với nhau vấn đề 2. Bài toán được giải quyết.
Nếu không 3 người họ chỉ trao đổi với nhau về vấn đề 3
10 tháng 5 2016
Gọi 17 người lần lượt là a1;a2;............;a17a1;a2;............;a17
Nhận thấy a1a1 viết cho 16 người về 3 đề tài ; theo nguyên lý dirichle , a1a1 sẽ viết cho 6 người về cùng một đề tài ; giả sử đó là đề tài A ; các người nhận được là a2;a3;a4;a5;a6;a7a2;a3;a4;a5;a6;a7
Gọi 7 điểm trên mặt phẳng tương ứng với các người ở trên
Tô màu các cạnh và đường chéo của đa giác nối bởi a1a1 và a2;.....a7a2;.....a7 bởi màu đỏ
Xét đa giác a2...........a7a2...........a7 được tô bởi 2 màu xanh và vàng ( vì nếu có một cạnh tô bởi màu đỏ thì ta có đpcm )
Tổng số cạnh và đường chéo của lục giác này là 15
Nên tồn tại 1 màu được tô 8 lần
Vì một điểm aiai trong 6 điểm này nối với 5 điểm còn lại chỉ được 5 đường thẳng , nên ta có đpcm .
PL
Phạm Lập Thăng
VIP
29 tháng 7
Theo nguyên lý Dirichlet thì 1 đề tài có ít nhất [(6-1) / (2)] +1 = 3 nhà khoa học trao đổi
HQ
Hà Quang Minh
Giáo viên
10 tháng 10 2023
- Mai đang điều tra về vấn đề các loại kem được khách hàng yêu thích.
- Dữ liệu thu thập gồm:
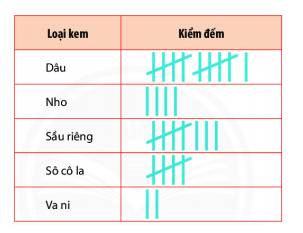
+ Các loại kem yêu thích của khách hàng gồm: Dâu, nho, sầu riêng, sô cô la, vani.
+ Kem dâu được 11 khách hàng yêu thích, kem nho được 4 khách hàng yêu thích, kem sầu riêng được 8 khách hàng yêu thích, kem sô cô la được 5 khách hàng yêu thích, kem va ni được 2 khách hàng yêu thích.
24 tháng 5 2020
Ta có số trận đã đấu của mỗi người có thể là 0,1,2,3,4. Nhưng vì không thể có cùng lúc một người đã đấu 4 ván và một người chưa đấu trận nào.
\(\Rightarrow\)Có tối đa 4 loại số trận đã đấu.
\(\rightarrow\)Theo nguyên lí Direcle tồn tại 2 dối thủ có số trận bằng nhau trong thời gian thi đấu.
25 tháng 1 2023
Ta có số trận đã đấu của mỗi người có thể là 0, 1, 2, 3, 4. Nhưng vì không thể có cùng lúc một người đã đấu 4 trận và một người chưa đấu trận nào
=> có tối đa 4 loại số trận đã đấu.
Vận dụng nguyên lý chuồng bồ câu ta có ít nhất có 2 người có cùng số trận đã đấu.
đây mà là lp 6 ak cậu
Bạn tham khảo:
https://olm.vn/hoi-dap/detail/6505989783.html