Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu là kết quả của việc sắp xếp 10 người theo 1 thứ tự.
⇒ n(Ω) = P10 = 10! = 3 628 800.
a) Gọi M: “A và B đứng liền nhau”
* Coi A và B là một phần tử X.
Số cách xếp X và 8 người khác thành hàng dọc là: 9!
Số cách xếp hai người A và B là: 2!= 2 cách
Theo quy tắc nhân có: 9!.2= 725760 cách xếp thỏa mãn
Xác suất của biến cố M là: 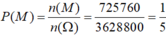
b) Gọi N: “Trong hai người đó có một người đứng ở vị trí số 1 và một người kia đứng ở vị trí cuối cùng”.
+ Sắp xếp vị trí cho A và B: Có 2 cách
+ Sắp xếp vị trí cho 8 người còn lại: có 8! cách
⇒ Theo quy tắc nhân: n(N) = 2.8!
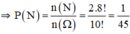

Chọn C
Ta có: ![]()
Gọi A là biến cố “trong 3 người được chọn đó không có 2 người ngồi kề nhau”
=> A ¯ là biến cố “trong 3 người đươc chọn có ít nhất 2 người ngồi kề nhau”
![]()

TH 1: 3 người ngồi kề nhau có 13 cách chọn.
TH 2: có 2 người ngồi cạnh nhau
- Hai người ngồi cạnh nhau ngồi đầu hàng có 2 cách chọn, với mỗi cách chọn như vậy có 12 cách chọn người còn lại vậy có: 2.12=24 cách.
- Hai người ngồi cạnh nhau không ngồi đầu hàng có 12 cách chọn, với mỗi cách chọn như vậy có 11 cách chọn người còn lại vậy có: 11.12=132 cách.
![]()
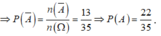

Chọn D
Tổng có 3 + 4 + 5 = 12 quyển sách được sắp xếp lên một giá sách có 3 ngăn (có 2 vách ngăn). Vì vậy, ta coi 2 vách ngăn này như 2 quyển sách giống nhau. Vậy số phần tử không gian mẫu ![]()
Gọi A là biến cố : “ Sắp xếp các 12 quyển sách lên giá sao cho không có bất kỳ hai quyển sách toán nào đứng cạnh nhau”.
+) Xếp 9 quyển sách ( lý và hóa) cùng 2 vách ngăn có 11 ! 2 ! cách
+) Lúc này, có 12 “khoảng trống” ( do 9 quyển sách ( lý và hóa) cùng 2 vách ngăn tạo ra) để xếp 3 quyển sách toán vào sao cho mỗi quyển vào một “khoảng trống” có A 12 3 cách.
Vậy có tất cả
11
!
2
!
.
A
12
3
cách. Suy ra 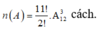
Vậy xác suất để không có bất kỳ hai quyển sách toán nào đứng cạnh nhau là:
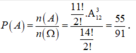

Chọn D
Giá có 3 ngăn như vậy có 2 vách ngăn, coi 2 vách ngăn này là 2 quyển sách giống nhau. Khi đó
bài toán trở thành xếp 14 quyển sách (2 quyển “VÁCH NGĂN” giống nhau) vào 14 vị trí. Đầu
tiên chọn 2 vị trị trí xếp vách ngăn là C 14 2 , 12 vị trí còn lại xếp 12 quyển sách là 12!. Vậy không gian mẫu là C 14 2 .12!.
Gọi A là biến cố “không có bất kì hai quyển sách toán nào đứng cạnh nhau”. Ta tìm số cách xếp thỏa mãn A
Đầu tiên ta xếp 11 quyển sách gồm 4 quyển lí, 5 quyển hóa và 2 quyển “VÁCH NGĂN”. Cũng
như trên, ta chọn 2 vị trí xếp 2 quyển “VÁCH NGĂN” trước là C 11 2 sau đó xếp 9 quyển còn lại là 9!. Vậy số cách xếp 11 quyển này là C 11 2 .9!. Sau khi xếp xong 11 quyển này thì sẽ có sẽ có 12 khe. Ta chọn 3 khe để xếp 3 quyển toán còn lại, là A 12 3 .
Vậy số cách thỏa mãn biến cố A là . C 11 2 .9!. A 12 3
Vậy  .
.

a.
Xếp 4 bạn nữ cạnh nhau: \(4!\) cách
Coi 4 bạn nữ là 1 bạn, xếp với 6 bạn nam: \(7!\) cách
Theo quy tắc nhân ta có: \(4!.7!\) cách
b.
Xếp 6 bạn nam: \(6!\) cách
6 bạn nam tạo thành 7 khe trống, xếp 4 nữ vào 7 khe trống này: \(C_7^4\) cách
\(\Rightarrow6!.C_7^4\) cách
c. Do có 6 nam và 4 nữ nên ko thể tồn tại cách xếp xen kẽ nam nữ (luôn có ít nhất 2 nam đứng cạnh nhau)
d.
Xếp 4 nữ cạnh nhau: \(4!\) cách
Xếp 6 nam cạnh nhau: \(6!\) cách
Hoán vị nhóm nam và nữ: \(2!\) cách
\(\Rightarrow4!.6!.2!\) cách

Số khả năng chọn ngẫu nhiên 3 người từ 6*2= 12 người là C 12 3 = 220
b. Gọi B là biến cố :” trong 3 người được chọn không có cặp vợ chồng nào” thì B ¯ là biến cố :” có đúng một cặp vợ chồng trong ba người được chọn”
![]()
( vì có 3 cách chọn cặp vợ chồng, và 10 cách chọn người thứ 3 trong số 10 người còn lại) nên
![]()
Chọn D

\(n\left(\Omega\right)=C^4_{10}=210\)
A: "Không chọn được hai chiếc nào tạo thành một đôi".
\(\overline{A}\): "Chọn được ít nhất hai chiếc tạo thành một đôi".
\(n\left(\overline{A}\right)=C^1_5\cdot C_8^2=140\).
\(n\left(A\right)=210-140=70\).
\(P\left(A\right)=\dfrac{70}{210}=\dfrac{1}{3}\).



Đáp án B
Có n ( Ω ) = C 12 3
Giả sử chọn 3 người có số thứ tự trong hàng lần lượt là a, b, c
Theo giả thiết ta có: a < b < c, b – a > 1, c – b > 1, a , b , c ∈ { 1 , 2 , . . . , 12 } .