K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
21 tháng 4 2017
lời giải
theo phương pháp chia nhỏ xét
\(f\left(x\right)=x^5-x^2-2x-1\)
\(f'\left(x\right)=5x^4-2x-2\)
\(f''\left(x\right)=20x^3-2\)
1) xét f'(x)
\(f''\left(x\right)=0\Rightarrow x=\sqrt[3]{\dfrac{1}{10}}\Rightarrow f'\left(x\right)\)
xét hàm f'(x) nếu có chỉ có 2 nghiệm trái dấu
f''(x) \(\left\{{}\begin{matrix}f''\left(x\right)< 0\\x\le0\end{matrix}\right.\)
Vậy điểm cực đại f(x) có hoành độ xcd<0
\(\left\{{}\begin{matrix}f'\left(-1\right)=5>0\\f'\left(0\right)=-2< 0\\f'\left(1\right)=1>0\end{matrix}\right.\) vậy f'(x) có hai nghiệm \(\left[{}\begin{matrix}x_{cđ}=\left(-1,0\right)\\x_{ct}=\left(0,1\right)\end{matrix}\right.\)
Ta lại có
\(f\left(x\right)=\dfrac{x}{5}.f'\left(x\right)-\dfrac{1}{5}\left(3x^2+8x+5\right)\)
\(\Rightarrow f\left(x_{cd}\right)=-\dfrac{1}{5}\left(x^2+8x-5\right)\)
{a-b+c=0} \(\Rightarrow f\left(x_{cd}\right)\le0..khi..\left[{}\begin{matrix}x\le-\dfrac{5}{3}\\x\ge-1\end{matrix}\right.\)
Khi \(-1< x< 0\Rightarrow f\left(cđ\right)< 0\)
\(\Rightarrow f\left(x\right)\) có nghiệm duy nhất --> dpcm
p/s:
nếu làm tổng thể \(f\left(x_{xd}\right).f\left(x_{ct}\right)>0\) ra bậc bốn rất khó khăn trong việc giải BPT
31 tháng 1 2018
Lời giải sau đây có lẽ đơn giản hơn:
Viết lại phương trình đã cho dưới dạng \(x^5=\left(x+1\right)^2\). Từ đó nếu \(x\) là nghiệm của phương trình thì \(x\ge0\).
Hơn nữa, \(x\ge0\Rightarrow x+1\ge1\Rightarrow x^5=\left(x+1\right)^2\ge1\Rightarrow x\ge1\) . Như vậy mọi \(x< 1\) đều không phải là nghiệm của phương trình.
Xét \(x\ge1\), ta có \(f'\left(x\right)=5x^4-2x-2=2x\left(x^3-1\right)+2\left(x^4-1\right)+1>0\). Do đó hàm số
\(f\left(x\right)=x^5-x^2-2x-1\) đồng biến trong khoảng \([1;+\infty)\). Ngoài ra \(f\left(1\right)=-3;f\left(2\right)=23\) nên phương trình \(f\left(x\right)=0\) có duy nhất một nghiệm (trong khoảng \(\left(1;2\right)\)).
CM
30 tháng 10 2017
Đáp án: B.
Các phương trình còn lại có nhiều hơn một nghiệm:
(x - 5)( x 2 - x - 12) = 0 có các nghiệm x = 5, 4, -3.
sin 2 x - 5sinx + 4 = 0 ⇔ sinx = 1, có vô số nghiệm
sinx - cosx + 1 = 0 có các nghiệm x = 0, x = 3 π /2
CM
31 tháng 5 2019
Đáp án: B.
Các phương trình còn lại có nhiều hơn một nghiệm:
(x - 5)( x 2 - x - 12) = 0 có các nghiệm x = 5, 4, -3.
sin 2 x - 5sinx + 4 = 0 ⇔ sinx = 1, có vô số nghiệm
sinx - cosx + 1 = 0 có các nghiệm x = 0, x = 3π/2.
CM
16 tháng 6 2018
Đáp án D.
Điều kiện cần để phương trình f
Do thay x bởi –x thì phương trình không đổi nên điều kiện cần để phương trình có nghiệm duy nhất là x = 0 => m = –1
Thử lại với m = –1 thỏa mãn nên D đúng.
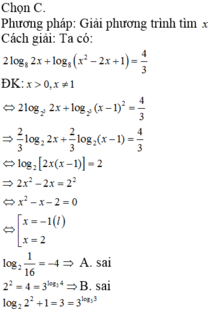
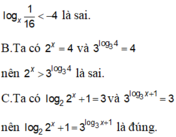
Ta có \(x^5-x^2-2x-1=0\Leftrightarrow x^5=\left(x+1\right)^2\).
Ta thấy nếu x là 1 nghiệm của pt trên thì x \(\geq\) 0. Từ đó \(\left(x+1\right)^2\ge1\Rightarrow x^5\ge1\Rightarrow x\ge1\).
Xét hàm số \(f\left(x\right)=x^5-x^2-2x-1=0\) trên khoảng \([1;+\infty)\). Ta có \(f'\left(x\right)=5x^4-2x-2=x^4+\left(2x^4-2x\right)+\left(2x^4-2\right)>0\) nên hàm số đồng biến trên khoảng \([1;+\infty)\).
Mặt khác ta có f(x) liên tục trên đoạn \(\left[1;2\right]\) và \(f\left(1\right).f\left(2\right)< 0\) nên hàm số có ít nhất một nghiệm trên khoảng \(\left[1;2\right]\).
Vậy phương trình đã cho có ít nhất một nghiệm.