N
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 3 2017
Ta có : \(2^{225}=\left(2^3\right)^{75}=8^{75}.\)
và : \(3^{151}=\left(3^3\right)^{75}\times3=9^{75}\times3\).
mà 975 > 875.
=> 2225 > 3151.
10 tháng 3 2017
ta có biêu thức trên\(\: < \frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{2012.2013}\)=\(\frac{2012}{2013}< 1\)
do dó biểu thức <1
18 tháng 11 2018
Ta có\(5a+3b\)chia hết cho 7 nên \(3\left(5a+3b\right)=15a+9b\)chia hết cho 7
Lại có \(15a+9b-5\left(3a-b\right)=15a+9b-15a+5b=14b\)
Vì \(14b\)chia hết cho 7 mà \(15a+9b=3\left(5a+3b\right)\)chia hết cho 7
Nên \(5\left(3a-b\right)\)chia hết cho 7
Vì 5 không chia hết cho 7 nên \(3a-b\)chia hết cho 7
Chúc bạn học tốt!
CM
2 tháng 5 2017
Sơ đồ con đường |
Lời giải chi tiết |
Áp dụng tính chất chia hết của một hiệu. |
Ta có: 36 ⋮ 9 ⇒ 36 36 ⋮ 9 9 ⋮ 9 ⇒ 9 10 ⋮ 9 ⇒ 36 36 + 9 10 ⋮ 9 |
CC
0
I
11 tháng 3 2020
cho \(M=1+3+3^2+...+3^{99}+3^{100}\)
=>\(M=1+\left(3+3^2+3^3\right)+...+\left(3^{98}+3^{99}+3^{100}\right)\)
\(=>M=1+3\left(1+3+3^2\right)+...+3^{98}\left(1+3+3^2\right)\)
\(=>M=1+13\left(3+...+3^{98}\right)\)
Mà \(13\left(3+3^{98}\right)⋮13\)
=> M chia cho 13 dư 1
11 tháng 3 2020
+) \(M=1+3+3^2+...+3^{99}+3^{100}\)
\(\Leftrightarrow M=\left(1+3+3^2\right)+\left(3^3+3^4+3^5\right)+...+\left(3^{98}+3^{99}+3^{100}\right)\)
\(\Leftrightarrow M=\left(1+3+9\right)+3^3\left(1+3+9\right)+....+3^{98}\left(1+3+9\right)\)
\(\Leftrightarrow M=13+3^3\cdot14+....+3^{98}\cdot14\)
\(\Leftrightarrow M=13\left(1+3^3+....+3^{98}\right)\)
=> M chia 13 dư 0
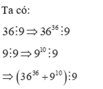
Cách 1
Ta có :
3636-910⋮9 vì các số hạng đều chia hết cho 9 .
Mặt khác :
3636có tận cùng là 6
910=(92)5=815có tận cùng là1
=>3636-910có tận cùng là 6 - 1 = 5
=>3636-910 chia hết cho 5
Mà (5 ; 9 ) = 1
=>336-910chia hết cho 45
Cách 2:
Vì 45=9x5
=> 3636-910 chia hết cho 9 (1) (vì 3636 và 910 đều chia hết cho 9)
3636 tận cùng là 6 (số tận cùng bằng 6 nâng lên luỹ thừa n (n nguyên dương) thì kết quả cũng tận cùng là 6)
910 tận cùng là 1 (9 luỹ thừa m với m chẵn luôn tận cùng là 1)
=> 3636-910 tận cùng là 5 và do đó nó chia hết cho 5 (2)
Vì 5 và 9 là 2 số nguyên tố cùng nhau nên từ (1),(2) => 3636-910chia hết cho 45.
NHỚ TK MK ĐÓ
Để hiệu này chia hết cho 45 thì phải chia hết cho 5 và 9 nhé bạn
_ Chia hết cho5
Xét chữ số tận cùng:
3636= (...6) có tận cùng là 6
910= 92x5=\(\left(9^2\right)^5\)=( ...1) có tận cùng là 1
\(\Rightarrow\)(...6)-(...1)=(...5) sẽ chia hết cho 5 (1)
-Chia hết cho 9
36 \(⋮\)9 suy ra \(^{36^{36}⋮9}\) (2)
Từ (1) và (2) suy ra ......(bạn tự kết luận nhé)
:))))))