Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dễ mà bạn :)) cái này dùng qui tắc công với chèn điểm là nuột =)
a) \(\overrightarrow{PQ}+\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{NP}+\overrightarrow{PQ}+\overrightarrow{MN}\)
\(=\overrightarrow{NQ}+\overrightarrow{MN}=\overrightarrow{MN}+\overrightarrow{NQ}=\overrightarrow{MQ}\left(đpcm\right)\)
( quá chi tiết rồi nha bạn... )
b) Ta có: \(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{MQ}+\overrightarrow{QN}\)
\(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}+\overrightarrow{NQ}+\overrightarrow{QN}\)
\(\Rightarrow\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}\left(đpcm\right)\)

Do \(\overrightarrow{NP}=\overrightarrow{DC}\); \(\overrightarrow{AM}=\overrightarrow{BA}\Rightarrow\overrightarrow{MA}=\overrightarrow{AB}\).
Do tứ giác ABCD là hình bình hành nên \(\overrightarrow{AB}=\overrightarrow{DC}\).
Vì vậy \(\overrightarrow{NP}=\overrightarrow{MA}\) nên tứ giác NPAM là hình bình hành.
Vì vậy \(\overrightarrow{PA}=\overrightarrow{NM}\). (1)
Mà \(\overrightarrow{MN}=\overrightarrow{DA}\) suy ra \(\overrightarrow{NM}=\overrightarrow{AD}\) . (2)
Mặt khác \(\overrightarrow{AD}=\overrightarrow{BC}\) (do tứ giác ABCD là hình bình hành). (3)
Từ (1);(2);(3) suy ra:\(\overrightarrow{PA}=\overrightarrow{BC}\).
Mà \(\overrightarrow{PQ}=\overrightarrow{BC}\Rightarrow\overrightarrow{PQ}=\overrightarrow{PA}\).
Vì vậy hai điểm A và Q trùng nhau nên \(\overrightarrow{AQ}=\overrightarrow{0}\).

a.\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}\)
VT:\(\overrightarrow{AB}+\overrightarrow{CD}\)
=\(\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{CA}+\overrightarrow{AD}\)
=\(\overrightarrow{AB}+\overrightarrow{CB}=0\left(đpcm\right)\)
b.\(\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{EA}=\overrightarrow{ED}+\overrightarrow{CB}\)
\(\Leftrightarrow\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{EA}+\overrightarrow{DE}+\overrightarrow{BC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{EA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AE}+\overrightarrow{EA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{0}=\overrightarrow{0}\left(LĐ\right)\)

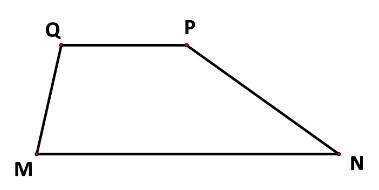
Do MQ và PN không song song với nhau nên \(\overrightarrow {MQ} \ne k\overrightarrow {NP} \). Vậy loại B và D.
Ta có: \(\overrightarrow {MN} ,\overrightarrow {PQ} \)là hai vecto ngược hướng và \(\left| {\overrightarrow {MN} } \right| = 2\left| {\overrightarrow {PQ} } \right|\)
Suy ra \(\overrightarrow {MN} = - 2\overrightarrow {PQ} \)
Vậy chọn C.


