Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) aaa=a.111=a.(3.37)
=>aaa bao giờ cũng chia hết cho 37
b) aaaaaa=a.111111=a.(3.37037)
=> aaaaaa bao giờ cũng chia hết cho 3
c) abcabc=abc.1001=abc.(7.13.11)
=> abcabc bao giờ cũng chia hết cho 13;11
d) ab+ba=(10a+b)+(10b+a)=(10a+a)+(10b+b)=11a+11b
=> ab+ba chia hết cho 11
ủng hộ nha
a) aaa = 111a = 37 . 3 . a
b) aaaaaa = 111111a = 37037 . 3 . a
c) abcabc = 1001abc = 77.13 . abc
abcabc = 1001abc = 77.13.abc = 7 .11.13.abc
d) (ab + ba) = 10a + b + 10b + a =11a + 11b = 11.(a+b)

a) aaaaaa = a . 111111 = a .15873 . 7 = ( a . 15873 ) . 7 chia hết cho 7
Vậy aaaaaa luôc chia hết cho 7
b)abcabc = abc . 1001 = abc . 91.11=( abc . 91 ) . 11 chia hết cho 11
Vậy abcabc bao giờ cũng chia hết cho 11

Tó biết làm mỗi 2 bài trên thui
1 ) aaa aaa = a . 111 111 = a . 11 . 10101 => chia hết cho 11
2 ) abc abc = abc . 1001 = abc . 11 . 91 = > chia hết cho 11
làm theo cách thầy dạy chứ hoàn toàn ko nhìn sách giải nhé

abc abc=abc.1000+abc=abc.(1000+1)
=abc.1001=abc.91.11
vì 11 chia hết cho 11=>abc.91.11 chia hết cho 11
vậy số abcabc lúc nào cũng chia hết cho 11

a, gọi 3 số tự nhiên liên tiếp là a;a+1;a+2 (a thuộc N)
tổng của chúng là : a + a + 1 + a + 2
= 3a + 3
= 3(a + 1) ⋮ 3
b, gọi 4 số tự nhiên liên tiếp là : b,b+1;b+2;b+3 (b thuộc N)
ta có tổng của chúng là :
b + b + 1 + b + 2 + b + 3
= 4b + 6
4b ⋮ 4; 6 không chia hết cho 4
=> 4b + 6 không chia hết cho 4
c, aaaaaa = 111111.a
= 15873.7.a ⋮ 7
d, abc abc
= 100000a + 10000b + 1000c + 100a + 10b + c
= 100100a + 10010b + 1001c
= 1001(100a + 10b + c)
= 11.91(100a + 10b + x) ⋮ 11
e, aaa = a.111 = a.3.37 ⋮ 37
f, ab - ba
= 10a + b - 10b - a
= 9a - 9b
= 9(a-b) ⋮ 9

a) aa = a.11 chia hết cho 11
b) aaa = 100.a+10 a+a = 111.a chia hết cho 37 (vì 111 chia hết cho 37)
c) aaaaaa = 111111.a chia hết cho 37 (vì 111111 chia hết cho 37)
d) abcabc = 100000a+10000b+1000c+100a+10b+c = 100100.a+10010b+1001c
ta thấy 100100.a chia hết cho 11 ( vì 100100 chia hết cho 11)
10010b chia hết cho 11 ( vì 10010 chia hết cho 11)
1001c chia hết cho 11 ( vì 1001 chia hết cho 11)
Vậy 100100.a+10010b+1001c chia hết cho 11 hay abcabc chia hết cho 11
e) C aaaaaa = 111111a chia hết cho 7 ( 111111 chia hết cho 7)

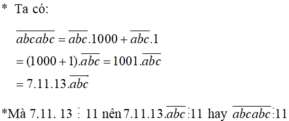
a) Ta có : abcabc = abc000 + abc
= abc x 1000 + abc
= abc x (1000 + 1)
= abc x 1001
= abc x 11 x 91 \(⋮\) 11
=> abcabc \(⋮\) 11 (đpcm)
b) Ta có : ab + ba
= 10a + b + 10b + a
= (10a + a) + (10b + b)
= 11a + 11b
= 11(a + b) \(⋮\) 11
=> ab + ba \(⋮\) 11 (đpcm)