HL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 9 2021
\(\left(\dfrac{2}{3}\right)^2\left(\dfrac{2}{3}\right)^4=\left(\dfrac{2}{3}\right)^{2+4}=\left(\dfrac{2}{3}\right)^6=\dfrac{2^6}{3^6}=\dfrac{64}{729}\)
HN
0
5 tháng 1 2022
\(\text{Bài 1:a)}25\dfrac{3}{19}.\left(-\dfrac{4}{5}\right)-35\dfrac{3}{19}.\left(-\dfrac{4}{5}\right)\)
\(=\dfrac{478}{19}.\left(-\dfrac{4}{5}\right)-\dfrac{668}{19}.\left(-\dfrac{4}{5}\right)\)
\(=\left(-\dfrac{4}{5}\right).\left(\dfrac{478}{19}-\dfrac{668}{19}\right)\)
\(=\left(-\dfrac{4}{5}\right).\left(\dfrac{-190}{19}\right)\)
\(=\left(-\dfrac{4}{5}\right).\left(-10\right)=8\)
\(\text{b)}5:\left(-\dfrac{5}{2}\right)^2+\dfrac{2}{15}.\sqrt{\dfrac{9}{4}}-\left(-2021\right)^0+0,25\)
\(=5:\dfrac{25}{4}+\dfrac{2}{15}.\dfrac{3}{2}-1+\dfrac{1}{4}\)
\(=\dfrac{4}{5}+\dfrac{1}{5}-1+\dfrac{1}{4}\)
\(=1-1+\dfrac{1}{4}\)
\(=0+\dfrac{1}{4}=\dfrac{1}{4}\)
\(\text{Bài 2:a)}\dfrac{8}{5}-\dfrac{3}{5}:x=0,4\)
\(\dfrac{3}{5}:x=\dfrac{8}{5}-0,4=\dfrac{6}{5}\)
\(x=\dfrac{3}{5}.\dfrac{5}{6}=\dfrac{1}{2}\)
\(\text{b)}\left(3x-\dfrac{1}{2}\right)^2+\dfrac{21}{25}=1\)
\(\left(3x-\dfrac{1}{2}\right)^2\) \(=1-\dfrac{21}{25}=\dfrac{4}{25}=\pm\left(\dfrac{2}{5}\right)^2\)
\(\text{Vậy }3x-\dfrac{1}{2}=\dfrac{2}{5}\)
\(3x\) \(=\dfrac{2}{5}+\dfrac{1}{2}=\dfrac{9}{10}\)
\(x\) \(=\dfrac{9}{10}.\dfrac{1}{3}=\dfrac{3}{10}\)
\(\text{hoặc }3x-\dfrac{1}{2}=\dfrac{-2}{5}\)
\(3x\) \(=\left(\dfrac{-2}{5}\right)+\dfrac{1}{2}=\dfrac{1}{10}\)
\(x\) \(=\dfrac{1}{10}.\dfrac{1}{3}=\dfrac{1}{30}\)
\(\Rightarrow x\in\left\{\dfrac{3}{10};\dfrac{1}{30}\right\}\)
5 tháng 1 2022
Bài 2:
a: =>3/5:x=6/5
hay x=3/5:6/5=1/2
b: \(\Leftrightarrow\left(3x-\dfrac{1}{2}\right)^2=\dfrac{4}{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\dfrac{1}{2}=\dfrac{2}{5}\\3x-\dfrac{1}{2}=-\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{10}\\x=\dfrac{1}{30}\end{matrix}\right.\)
5 tháng 1 2022
Bài 4:
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB=CD
DH
14 tháng 7 2017
Thế méo nào cho lẻ độ @@
Giả sử \(\widehat{xOz}+\widehat{yOz}+\widehat{yOt}=250^o46'\)
mà \(\widehat{xOz}+\widehat{yOz}=180^o\)
\(\Rightarrow\widehat{yOt}=250^o46'-180^o=70^o46'\)
Mặt khác \(\widehat{yOt}=\widehat{xOz}\left(d.d\right)\Rightarrow\widehat{yOt}=\widehat{xOz}=70^o46'\)
Ta có:
\(\widehat{yOt}+\widehat{yOz}=180^o\Rightarrow\widehat{yOz}=180^o-70^o46'=109^o14'\)
mà \(\widehat{yOz}=\widehat{xOt}\left(d.d\right)\Rightarrow\widehat{yOz}=\widehat{xOt}=109^o14'\)
Vậy...........
Chúc bạn học tốt!!!
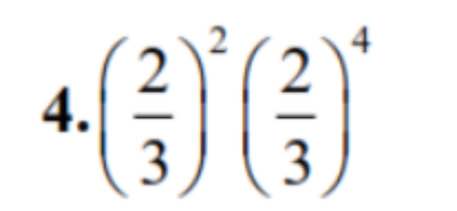
Lời giải:
\(x^2\geq 0, \forall x\in\mathbb{R}\)
\(x^8=(x^4)^2\geq 0, \forall x\in\mathbb{R}\)
\(\Rightarrow G(x)=2+7x^2+x^8\geq 2+7.0+0>0, \forall x\in\mathbb{R}\)
Như vậy, $G(x)\neq 0$ với mọi $x\in\mathbb{R}$. Suy ra đa thức $G(x)$ không có nghiệm thực.
Cảm ơn ạ