Chứng minh rằng nếu một hàm số liên tục trên (a;b] và trên [b; c) thì nó liên tục trên (a; c) ?

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

SG

Sách Giáo Khoa

10 tháng 4 2017

Chứng minh rằng nếu một hàm số liên tục trên (a;b] và trên [b; c) thì nó liên tục trên (a; c) ?

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 5 2022

undefined

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PT

Pham Trong Bach

7 tháng 10 2019

Chứng minh rằng nếu một hàm số liên tục trên (a; b] và trên [b; c) thì nó liên tục trên (a; c)

#Toán lớp 11

1

CM

Cao Minh Tâm

7 tháng 10 2019

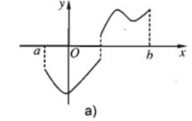
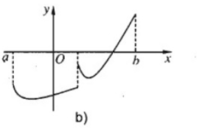
Vì hàm số liên tục trên (a; b] nên liên tục trên (a; b) và

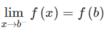Giải sách bài tập Toán 11 | Giải sbt Toán 11 (1)

Vì hàm số liên tục trên [b; c) nên liên tục trên (b; c) và

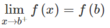Giải sách bài tập Toán 11 | Giải sbt Toán 11 (2)

Từ (1) và (2) suy ra f(x) liên tục trên các khoảng (a; b), (b; c) và liên tục tại x = b

(vì 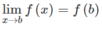Giải sách bài tập Toán 11 | Giải sbt Toán 11 ).

Nghĩa là nó liên tục trên (a; c)

PT

Pham Trong Bach

21 tháng 11 2018

Cho ví dụ về một hàm số liên tục trên (a; b] và trên (b; c) nhưng không liên tục trên (a; c)

#Toán lớp 11

1

CM

Cao Minh Tâm

21 tháng 11 2018

Xét hàm số

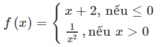
Giải sách bài tập Toán 11 | Giải sbt Toán 11

- Trường hợp x ≤ 0

f(x) = x + 2 là hàm đa thức, liên tục trên R nên nó liên tục trên (-2; 0]

- Trường hợp x > 0

f ( x ) = 1 / x 2 là hàm số phân thức hữu tỉ nên liên tục trên (2; 0) thuộc tập xác định của nó.

Như vậy f(x) liên tục trên (-2; 0] và trên (0; 2)

Tuy nhiên, vì 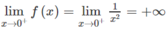Giải sách bài tập Toán 11 | Giải sbt Toán 11 nên hàm số f(x) không cógiới hạn hữu hạn tại x = 0. Do đó, nó không liên tục tại x = 0. Nghĩa là không liên tục trên (-2; 2)

SG

Sách Giáo Khoa

10 tháng 4 2017

Cho ví dụ về một hàm số liên tục trên (a; b] và trên (b;c) nhưng không liên tục trên (a; c) ?

#Toán lớp 11

1

Q

qwerty

11 tháng 4 2017

$\underset{x\rightarrow a^{+}}{lim}$ f(x) = f(a); $\underset{x\rightarrow b^{-}}{lim}$ f(x)= f(b).

PT

Pham Trong Bach

22 tháng 7 2018

Cho hàm số f x = 3 x + 2 n ế u x < - 1 x 2 - 1 n ế u x ≥ - 1 a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.b. Khẳng định nhận xét trên bằng 1 chứng...

#Toán lớp 11

1

CM

Cao Minh Tâm

22 tháng 7 2018

a) Đồ thị hàm số (hình bên).

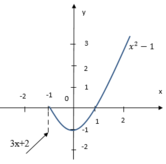
Bài 3 trang 141 sgk Đại Số 11 | Để học tốt Toán 11

Quan sát đồ thị nhận thấy :

+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).

+ f(x) không liên tục tại x = -1.

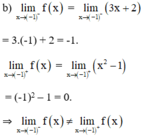
Bài 3 trang 141 sgk Đại Số 11 | Để học tốt Toán 11

⇒ không tồn tại giới hạn của f(x) tại x = -1.

⇒ Hàm số không liên tục tại x = -1.

LT

Lê Thiện

23 tháng 6 2019 - olm

Cho f (x) là hàm số liên tục trên [a ,b] và khả vi trên (a,b) .

Chứng minh rằng tồn tại số c thuộc (a,b) sao cho \(\frac{2}{a-c}\)< f'(c)cos(f(c)) <\(\frac{2}{b-c}\)

#Toán lớp 11

0

PT

Pham Trong Bach

26 tháng 10 2019

Cho hàm số y = f(x) xác định trên khoảng (a; b) chứa điểm x 0 Chứng minh rằng nếu lim x → x 0 f ( x ) - f ( x 0 ) x - x 0 = L thì hàm số f(x) liên tục tại điểm x 0 Đặt g ( x ) = f ( x ) ...

#Toán lớp 11

1

CM

Cao Minh Tâm

26 tháng 10 2019

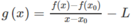
Đặt Giải sách bài tập Toán 11 | Giải sbt Toán 11

Suy ra g(x) xác định trên ( a ; b ) \ x 0 và 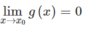Giải sách bài tập Toán 11 | Giải sbt Toán 11

Mặt khác, f ( x ) = f ( x 0 ) + L ( x − x 0 ) + ( x − x 0 ) g ( x ) nên

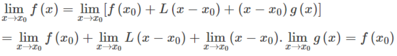
Giải sách bài tập Toán 11 | Giải sbt Toán 11

Vậy hàm số y = f(x) liên tục tại

PT

Pham Trong Bach

12 tháng 5 2018

Cho hàm số y=f(x) liên tục trên đoạn [a; b]. Nếu f(a).f(b) > 0 thì phương trình f(x) = 0 có nghiệm hay không trong khoảng (a; b)? Cho ví dụ minh hoạ.

#Toán lớp 11

1

CM

Cao Minh Tâm

12 tháng 5 2018

Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0 có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)

Ví dụ minh hoạ :

- f ( x ) = x 2 − 1 liên tục trên đoạn [−2;2], f(−2).f(2) = 9 > 0

Phương trình x 2 – 1 = 0 có nghiệm x = 1 hoặc x = -1 trong khoảng (-2; 2)

- f ( x ) = x 2 + 1 liên tục trên đoạn [-1; 1] và f(−1).f(1) = 4 > 0. Còn phương trình x 2 + 1 = 0 lại vô nghiệm trong khoảng (-1; 1)

DG

Đỗ Gia Huy

13 tháng 11 2023 - olm

Cho hàm số �:[�;�]→[�;�]f:[a;b]→[a;b] liên tục trên [�,�][a,b] với �<�a<b thỏa mãn ∣�(�)−�(�)∣<∣�−�∣∣f(α)−f(β)∣<∣α−β∣, ∀�,�∈[�;�]∀α,β∈[a;b] phân biệt. Chứng minh rằng ∃!�∈[�;�]:�(�)=�∃!γ∈[a;b]:f(γ)=γ (Ở đây kí hiệu ∃!∃! nghĩa là tồn tại duy nhất) #Toán lớp...

#Toán lớp 11

0

PT

Pham Trong Bach

11 tháng 11 2017

Nếu hàm số y = f(x) không liên tục trên đoạn [a; b] nhưng f(a).f(b) < 0 thì phương trình f(x) = 0 có nghiệm hay không trong khoảng (a; b)? Hãy giải thích câu trả lời bằng minh hoạ hình học.

#Toán lớp 11

1

CM

Cao Minh Tâm

11 tháng 11 2017

Nếu hàm số y = f(x) không liên tục trên đoạn [a; b] nhưng f(a).f(b) < 0 thì phươngtrình f(x) = 0 có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)

Minh hoạ hình hoạ (H.8):

Giải sách bài tập Toán 11 | Giải sbt Toán 11

Giải sách bài tập Toán 11 | Giải sbt Toán 11