TT
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 10 2023
a: \(A=4+2^2+2^3+...+2^{20}\)
=>\(2A=8+2^3+2^4+...+2^{21}\)
=>\(2A-A=2^{21}+2^{20}+...+2^4+2^3+8-2^{20}-2^{19}-...-2^3-2^2-4\)
\(=2^{21}+8-2^2-4=2^{21}\)
=>\(A=2^{21}\) là lũy thừa của 2
b:
\(B=3+3^2+3^3+...+3^{100}\)
=>\(3B=3^2+3^3+...+3^{101}\)
=>\(2B=3^{101}-3\)
=>\(2B+3=3^{101}\) là lũy thừa của 3
CG
0
15 tháng 11 2017
a, Có 2A = 4.2+2^3+2^4+...+2^21
A=2A-A=(4.2+2^3+2^4+...+2^21)-(4+2^2+2^3+...+2^20) = 4.2 + 2^21 - 4 - 2^2 = 2^21
=> A là lũy thừa cơ số 2
b, Có 3A=3^2+3^3+3^4+...+3^101
2A=3A-A=(3^2+3^3+3^4+....+3^101)-(3+3^2+3^3+....+3^100) = 3^101-3
=> 2A+3 = 3^101-3+3 = 3^101
=> A là lũy thừa của 3
k mk nha
AM
28 tháng 6 2015
A=4+22+23+...+220
Đặt B=22+23+...+220
=>2B=23+24+...+221
=>2B-B=221-22=221-4
=>A=4+B=4+221-4=221
=>A là lũy thừa của 2(ĐPCM)
b)A=3+32+33+...+3100
=>3A=32+33+...+3101
=>3A-A=3101-3
=>2A=3101-3
=>2A+3=3101-3+3=3101
Vậy 2A+3 là lũy thừa của 3(ĐPCM)
LM
0
OY
20 tháng 7 2021
A=3+32+33+...+3100
3A=32+33+...+3101
3A-A=(32+33+...+3101)-(3+32+33+...+3100)
2A=3101-3
2A+3=3101
DX
20 tháng 7 2021
\(A=3+3^2+3^3+...+3^{100}\)
\(\Rightarrow3A=3.\left(3+3^2+3^3+...+3^{100}\right)\)
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{101}\)
\(\Rightarrow3A-A=2A=\left[3^2+3^3+3^4+...+3^{101}\right]-\left[3+3^2+3^3+...+3^{100}\right]\)\(\Rightarrow2A=3^{101}-3\)
Theo đề bài ta có 2A + 3 = 3n ( \(n\in N\) )
\(\Rightarrow2A+3=3^{101}-3+3=3^n\)
\(\Rightarrow2A+3=3^{101}=3^n\)
\(\Rightarrow3^{101}=3^n\)
\(\Rightarrow101=n\) ( thỏa mãn điều kiện \(n\in N\)
Vậy n = 101
PT
1
CM
22 tháng 11 2018
Ta có: A = 3 + 3 2 + 3 3 + . . . + 3 100
=> 3 A = 3 2 + 3 3 + 3 4 + . . . + 3 101
=> 3 A - A = ( 3 2 + 3 3 + 3 4 + . . . + 3 101 ) - ( 3 + 3 2 + 3 3 + . . . + 3 100 )
=> 2 A = 3 2 + 3 3 + 3 4 + . . . + 3 101 - 3 - 3 2 - 3 3 - . . . - 3 100
2 A = 3 101 - 3 <=> 2 A + 3 = 3 101 , mà 2 A + 3 = 3 n
=> n = 101
20 tháng 12 2021
b: \(A=3\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\)
\(=13\left(3+...+3^{58}\right)⋮13\)
20 tháng 12 2021
\(a,\Leftrightarrow2A=8+2^3+2^4+...+2^{21}\\ \Leftrightarrow2A-A=8+2^3+2^4+...+2^{21}-4-2^2-2^3-...-2^{20}\\ \Leftrightarrow A=2^{21}+8-4-2^2=2^{21}\left(đpcm\right)\\ b,A=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+...+\left(3^{58}+3^{59}+3^{60}\right)\\ A=3\left(1+3+3^2\right)+3^4\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\\ A=\left(1+3+3^2\right)\left(3+3^4+...+3^{58}\right)\\ A=13\left(3+3^4+...+3^{58}\right)⋮13\)
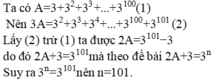
A = 3 + 32 + 33 + ........ + 3100
3A = 32 + 33 + 34 + ....... + 3101
3A - A = ( 32 + 33 + 34 + ....... + 3101 ) - ( 3 + 32 + 33 + ........ + 3100 )
2A = 3101 - 3
=> 2A + 3 = 3101 - 3 + 3
Vậy 2A là một lũy thừa của 3
Có 3A = 3^2+3^3+....+3^101
2A=3A-A = (3^2+3^3+....+3^101) - (3+3^2+....+3^100)
= 3^101 - 3
=> 2A + 3 = 3^101 - 3 + 3 = 3^101 là 1 lũy thừa của 3
=> ĐPCM