Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
Ta có AN = NB = AB/2 (Tính chất đường trung tuyến)
AM = MC = AC/2 (Tính chất đường trung tuyến)
Vì ∆ ABC cân tại A=> AB = AC nên AM = AN
Xét ∆BAM ;∆CAN có:
AM = AN (cm trên)
Góc A chung
AB = AC (∆ABC cân)
Nên suy ra ∆BAM = ∆CAN (c-g-c)
=> BM = CN ( 2 cạnh tương ứng)
A) Ta có AB2 + AC2 = BC2 => AB2 = BC2 - AC2 = 100 - 36 => AB = 8cm
B) AM = BM (Do CM là trung tuyến của tam giác ABC)
CM = MD (Theo đề bài)
góc AMC = BMD (hai góc đối đỉnh)
=> Tam giác MAC = tam giác MBD (cgc)
=> AC = BD (Hai cạnh tương ứng của hai tam giác bằng nhau)
C) Ta có BC + BD > CD
=> BC + AC > 2 CM
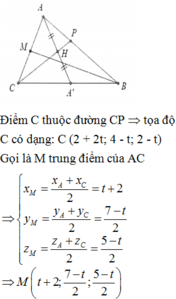
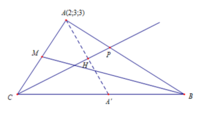
Xét (O) có
ΔCDM nội tiếp
CM là đường kính
DO đó: ΔCDM vuông tại D
Xét tứ giác ABCD có
\(\widehat{CDB}=\widehat{CAB}=90^0\)
Do đó: ABCD là tứ giác nội tiếp
b: \(\widehat{BCA}=\widehat{ADB}\)
mà \(\widehat{ADB}=\widehat{KCA}\)
nên \(\widehat{BCA}=\widehat{KCA}\)
hay CA là tia phân giác của góc KCB
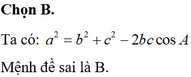
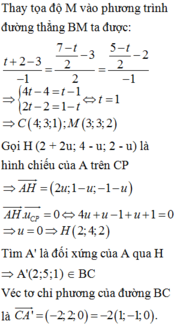
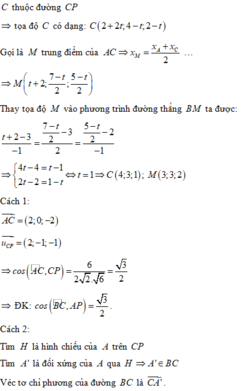
Bài 42 trang 73 sgk toán lớp 7- tập 2
Cập nhật lúc: 08/07/2014 17:21 pm Danh mục: Toán lớp 7
Chứng minh định líXem thêm: Tính chất ba đường phân giác của tam giác
42. Chứng minh định lí : Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân
Gợi ý : Trong ∆ABC, nếu AD vừa là đường trung tuyến vừa là đường phân giác thì kéo dài AD một đoạn AD1 sao cho DA1 = AD
Hướng dẫn:
Giả sử ∆ABC có AD là phân giác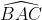
và DB = DC, ta chứng minh ∆ABC cân tại A
Kéo dài AD một đoạn DA1 = AD
Ta có: ∆ADC = ∆A1DC (c.g.c)
Nên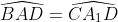
mà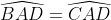
(gt)
=>
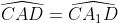
=> ∆ACA1 cân tại C
Ta lại có: AB = A1C ( ∆ADB = ∆A1DC)
AC = A1C ( ∆ACA1 cân tại C)
=> AB = AC
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân