K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CX
20 tháng 11 2021
Tham khảo
Chứng minh định lí là dùng suy luận để khẳng định kết luận (được suy ra từ giả thiết) là đúng. Một tính chất được khẳng định là đúng bằng suy luận được gọi là định lí. Định lí thường phát biểu dưới dạng: " Nếu A thì B " với A là giả thiết, là điều kiện cho biết; B là kết luận, là điều được suy ra.
CT
20 tháng 11 2021
TK:
Chứng minh định lí là dùng suy luận để khẳng định kết luận (được suy ra từ giả thiết) là đúng. Một tính chất được khẳng định là đúng bằng suy luận được gọi là định lí. Định lí thường phát biểu dưới dạng: " Nếu A thì B " với A là giả thiết, là điều kiện cho biết; B là kết luận, là điều được suy ra.
Giả thuyết là sự giải thích đề xuất cho một hiện tượng. Để một giả thuyết trở thành một giả thuyết khoa học, phương pháp khoa học yêu cầu cần có một sự kiểm định. Các giả thuyết khoa học thường được các nhà khoa học dựa vào những quan sát trước đó mà không thể giải thích được với các lý thuyết khoa học hiện có.
CM
6 tháng 7 2017
Ta có BC < BD mà C, D nằm cùng phía so với B ⇒ C nằm giữa B và D.
CM
2 tháng 11 2017
Đáp án A
Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận.
17 tháng 9 2023
a)
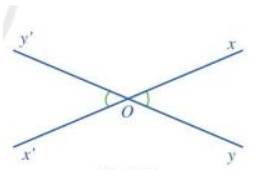
b)
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau
\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù
\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)
\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)
IM
7 tháng 10 2016
Cho 2 góc xOy và yOz kề bù .
Om ; On lần lượt là tia phân giác của 2 góc đó
\(\Rightarrow\begin{cases}\widehat{O_1}=\widehat{O_2}=\frac{1}{2}.\widehat{xOy}\\\widehat{O_3}=\widehat{O_4}=\frac{1}{2}.\widehat{yOz}\end{cases}\)
\(\Rightarrow\widehat{O_2}+\widehat{O_3}=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\frac{1}{2}.180^0=90^0\)
=> Đpcm
7 tháng 10 2016
* Vẽ hình: Vẽ hình hơi xấu chút! 
* Viết giả thiết, kết luận:
GT: - Góc xOz và góc yOz là hai góc kề bù
- Ot là tia phân giác của góc xOz
- Ot' là tia phân giác của góc yOz
KL: Góc tot' là 1 góc vuông
* Chứng minh:
Góc xOt = góc tOz = 1/2 . góc xOz (vì Ot là tia phân giác của góc xOz)
Góc yot' = góc t'Oz = 1/2 . góc yOz (vì Ot' là tia phân giác của góc yOz)
Góc xOz + góc yOz = 180 độ (vì 2 góc kề bù)
Vì góc xOz và góc yOz là 2 góc kề bù mà
Ot là tia phân giác xOz
Ot' là tia phân giác yOz
=> Tia Oz nằm giữa hai tia Ot và Ot' nên:
Góc tOt' = góc tOz + góc t'Oz = 1/2 . góc xOz + 1/2 . góc yOz = 1/2 . (góc xOz + góc yOz) = 1/2 . 180 độ = 90 độ
Vậy tOt' là 1 góc vuông.
14 tháng 9 2016
- Giả thuyết: cho góc tạo bởi 2 tia phân giác của 2 góc kề bù
- Kết luận: đó là 1 góc vuông
- Chứng minh:
Ta có hình vẽ:
Do Om là tia phân giác của góc zOy => góc \(zOm=mOy=\frac{1}{2}.zOy\)
Do On là tia phân giác của góc xOz => góc \(xOn=nOz=\frac{1}{2}.xOz\)
Ta có:
zOy + xOz = 180o (kề bù)
=> \(\frac{1}{2}.zOy+\frac{1}{2}.xOz=\frac{1}{2}.180^o\)
=> zOm + zOn = 90o
Lại có: zOn + zOm = mOn => mOn = 90o là góc vuông (đpcm)
17 tháng 9 2023
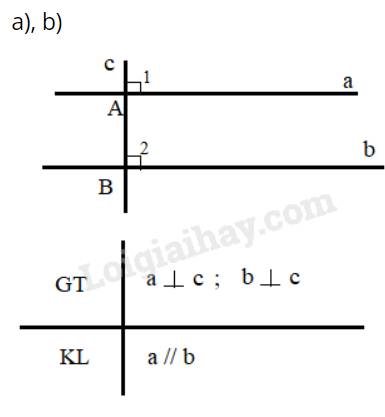
c) Giả sử có 2 đường thẳng phân biệt a,b cùng vuông góc với một đường thẳng c.
Ta có: \(\widehat {{A_1}} = \widehat {{B_2}}\), mà hai góc này ở vị trí đồng vị nên a//b (Dấu hiệu nhận biết 2 đường thẳng song song)
Như vậy, định lí trên có thể được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.
Trong toán học và logic, một định lý là một mệnh đề phi hiển nhiên đã được chứng minh là đúng, hoặc trên cơ sở dẫn xuất từ các tiên đề hoặc được chứng minh trên cơ sở lấy từ từ các định lý khác.
Tham khảo : Chứng minh định lí là dùng suy luận để khẳng định kết luận (được suy ra từ giả thiết) là đúng.