HT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DP
0
NT
1
DD
Đoàn Đức Hà
Giáo viên
21 tháng 11 2021
\(\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{100}}\)
\(=\frac{1}{\sqrt{1}}+\left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{4}}\right)+\left(\frac{1}{\sqrt{5}}+...+\frac{1}{\sqrt{9}}\right)+...+\left(\frac{1}{\sqrt{82}}+...+\frac{1}{\sqrt{100}}\right)\)
\(>\frac{1}{\sqrt{1}}+\left(\frac{1}{\sqrt{4}}+\frac{1}{\sqrt{4}}+\frac{1}{\sqrt{4}}\right)+\left(\frac{1}{\sqrt{9}}+...+\frac{1}{\sqrt{9}}\right)+...+\left(\frac{1}{\sqrt{100}}+...+\frac{1}{\sqrt{100}}\right)\)
\(>\frac{1}{1}+\frac{2}{2}+\frac{3}{3}+...+\frac{10}{10}=10\)
VM
20 tháng 11 2019
b) Ta có:
\(\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{99}+\sqrt{100}}\)
\(=\frac{\sqrt{1}-\sqrt{2}}{-1}+\frac{\sqrt{2}-\sqrt{3}}{-1}+...+\frac{\sqrt{99}-\sqrt{100}}{-1}\)
\(=\sqrt{2}-\sqrt{1}+\sqrt{3}-\sqrt{2}+...+\sqrt{100}-\sqrt{99}\)
\(=-\sqrt{1}+\sqrt{100}\)
\(=\left(-1\right)+10\)
\(=9.\)
Vì \(9=9.\)
\(\Rightarrow\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{99}+\sqrt{100}}=9\left(đpcm\right).\)
Chúc bạn học tốt!
Z
1
17 tháng 3 2020
Nhận thấy với mọi k \(\in\) N* ta có :
\(\left(\sqrt{k+1}-\sqrt{k}\right).\left(\sqrt{k+1}+\sqrt{k}\right)=\left(\sqrt{k+1}\right)^2-\left(\sqrt{k}\right)^2=k+1-k=1\)
\( \implies\)\(\frac{\left(\sqrt{k+1}-\sqrt{k}\right).\left(\sqrt{k+1}+\sqrt{k}\right)}{\sqrt{k+1}+\sqrt{k}}=\frac{1}{\sqrt{k+1}+\sqrt{k}}\)
\( \implies\) \(\frac{1}{\sqrt{k+1}+\sqrt{k}}=\sqrt{k+1}-\sqrt{k}\)
Thật vậy : \(\frac{1}{\sqrt{k}}=\frac{2}{2.\sqrt{k}}>\frac{2}{\sqrt{k}+\sqrt{k+1}}=2.\left(\sqrt{k+1}-\sqrt{k}\right)\)
Thay k = 1 ; 2 ; 3 ; ....; 64 ta được :
\(\frac{1}{\sqrt{1}}>2.\left(\sqrt{1+1}-\sqrt{1}\right)=2.\left(\sqrt{2}-\sqrt{1}\right)=2.\sqrt{2}-2.\sqrt{1}\)
\(\frac{1}{\sqrt{2}}>2.\left(\sqrt{2+1}-\sqrt{2}\right)=2.\left(\sqrt{3}-\sqrt{2}\right)=2.\sqrt{3}-2.\sqrt{2}\)
\(\frac{1}{\sqrt{3}}>2.\left(\sqrt{3+1}-\sqrt{3}\right)=2.\left(\sqrt{4}-\sqrt{3}\right)=2.\sqrt{4}-2.\sqrt{3}\)
. . . . . . . . . . . . . . . . . . . . . .
\(\frac{1}{\sqrt{64}}>2.\left(\sqrt{64+1}-\sqrt{64}\right)=2.\left(\sqrt{65}-\sqrt{64}\right)=2.\sqrt{65}-2.\sqrt{64}\)
Cộng vế với vế ta được :
\(\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+...+\frac{1}{\sqrt{64}}>2.\sqrt{2}-2.\sqrt{1}+2.\sqrt{3}-2.\sqrt{2}+....+2.\sqrt{65}-2.\sqrt{64}\)
\( \implies\) \(\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+...+\frac{1}{\sqrt{64}}>2.\sqrt{65}-2.\sqrt{1}=2.\left(\sqrt{65}-\sqrt{1}\right)\) ( * )
Ta thấy : \(\sqrt{65}>\sqrt{64}\)
\( \implies\) \(\sqrt{65}-\sqrt{1}>\sqrt{64}-\sqrt{1}\)
\( \implies\) \(\sqrt{65}-\sqrt{1}>7\)
\( \implies\) \(2.\left(\sqrt{65}-\sqrt{1}\right)>2.7\)
\( \implies\) \(2.\left(\sqrt{65}-\sqrt{1}\right)>14\) ( ** )
Từ ( * ) ; ( ** )
\( \implies\) \(\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{64}}>14\left(đpcm\right)\)
17 tháng 7 2022
Bài 6:
Để B là số nguyên thì \(\sqrt{x}-2+3⋮\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}-2\in\left\{1;-1;3\right\}\)
hay \(x\in\left\{9;1;25\right\}\)
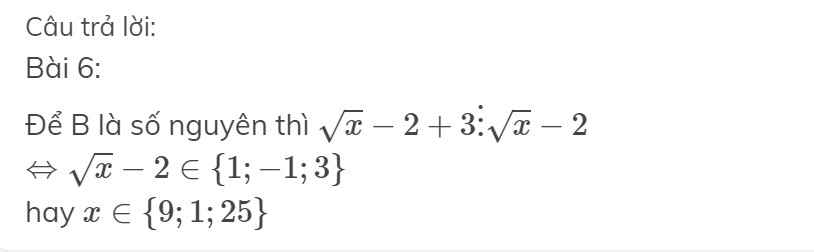
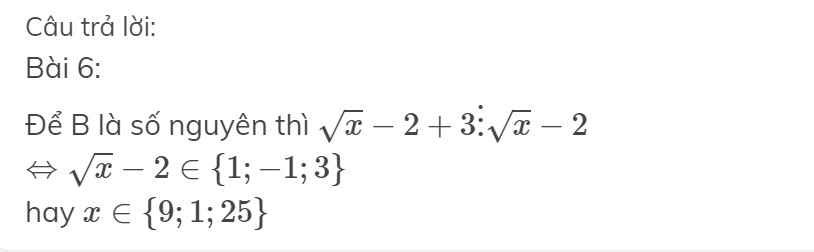
Ý bạn là \(18< \frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+...+\frac{1}{\sqrt{100}}< 19\) ?
Ta có:
\(A=\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+...+\frac{1}{\sqrt{100}}=\frac{2}{2\sqrt{1}}+\frac{2}{2\sqrt{2}}+...+\frac{2}{2\sqrt{100}}\)
\(\Rightarrow A>\frac{2}{1+\sqrt{2}}+\frac{2}{\sqrt{2}+\sqrt{3}}+...+\frac{2}{\sqrt{100}+\sqrt{101}}\)
\(\Rightarrow A>\frac{2\left(\sqrt{2}-1\right)}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}+\frac{2\left(\sqrt{3}-\sqrt{2}\right)}{\left(\sqrt{3}-\sqrt{2}\right)\left(\sqrt{3}+\sqrt{2}\right)}+...+\frac{2\left(\sqrt{101}-\sqrt{100}\right)}{\left(\sqrt{101}-\sqrt{100}\right)\left(\sqrt{101}+\sqrt{100}\right)}\)
\(\Rightarrow A>2\left(\sqrt{2}-1+\sqrt{3}-2+...+\sqrt{101}-\sqrt{100}\right)\)
\(\Rightarrow A>2\left(\sqrt{101}-1\right)>2\left(\sqrt{100}-1\right)=18\)
Tương tự:
\(A=1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{100}}=1+\frac{2}{2\sqrt{2}}+\frac{2}{2\sqrt{3}}+...+\frac{2}{2\sqrt{100}}\)
\(\Rightarrow A< 1+\frac{2}{1+\sqrt{2}}+\frac{2}{\sqrt{2}+\sqrt{3}}+...+\frac{2}{\sqrt{99}+\sqrt{100}}\)
Nhân liên hợp tử mẫu và rút gọn ta được (giống chứng minh >18 bên trên):
\(A< 1+2\left(\sqrt{2}-1+\sqrt{3}-\sqrt{2}+...+\sqrt{100}-\sqrt{99}\right)\)
\(\Rightarrow A< 1+2\left(\sqrt{100}-1\right)=1+18=19\)
\(\Rightarrow18< A< 19\) (đpcm)
giup minh vs