NL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
1
26 tháng 9 2015
abcabc = abc x 1000 + abc
= abc x ( 1000 + 1)
= abc x 1001
= abc x 11 x 91
= > abc : 11
ZH
3
HP
30 tháng 12 2015
913+1=94*3+1+1=94*3*9+1=...............................1*9+1=..............................9+1=...........................0
Vì số có chữ số tận cùng là 0 nên số đó chia hết cho cả 2 và 5
nên 913+1 chia hết cho cả 2 và 5
31 tháng 7 2015
Nếu Chia hết cho 10 thì chia hết cho cả 2 và 5
Ta có: 316 = (32)8 = 98
Ta có: nếu 9chẵn tận cùng là 1
=> 98 = (..........1)
=> 98 - 1 = (.......1 - 1)
98 = (............0) nên chia hết cho 10
Vậy 316 chia hết cho 10
PA
0
PH
1
31 tháng 12 2019
Ta có: \(3^4=81\) có chữ số tận cùng là 1.
=> 2003\(^4\)có chữ số tận cùng là 1
=> \(2003^{400}\)có chữ số tận cùng là 1
lại có: \(2001^{4000}\)có chữ số tận cùng là 1
=> \(2003^{4000}-2001^{4000}\)có chữ số tận cùng là 0
=> \(2003^{4000}-2001^{4000}\) chia hết cho 2 và chia hết cho 5.
CM
9 tháng 1 2018
Chứng minh rằng:
a) Ta có: 102002+8 = 10...000 (2002 số 0) + 8 = 10...008 (2001 số 0) có 8 tận cùng nên chia hết cho 2 và tổng các chữ số của nó là: 1+0+...+0+0+8=9 nên chia hết cho 9
Vậy 102002 +8 chia hết cho 2 và 9.
b) Tương tự: = 10...014 (2002 số 0) có 4 tận cùng nên chia hết cho 2
và tổng các chữ số của nó là: 1+0+...+0+1+4=6 nên chia hết cho 3
Vậy 102004 +14 chia hết cho 2 và 3.
BL
3
30 tháng 12 2015
913+1=...0 chia hết cho 2 và 5
Vậy 913+1 chia hết cho 2 và 5
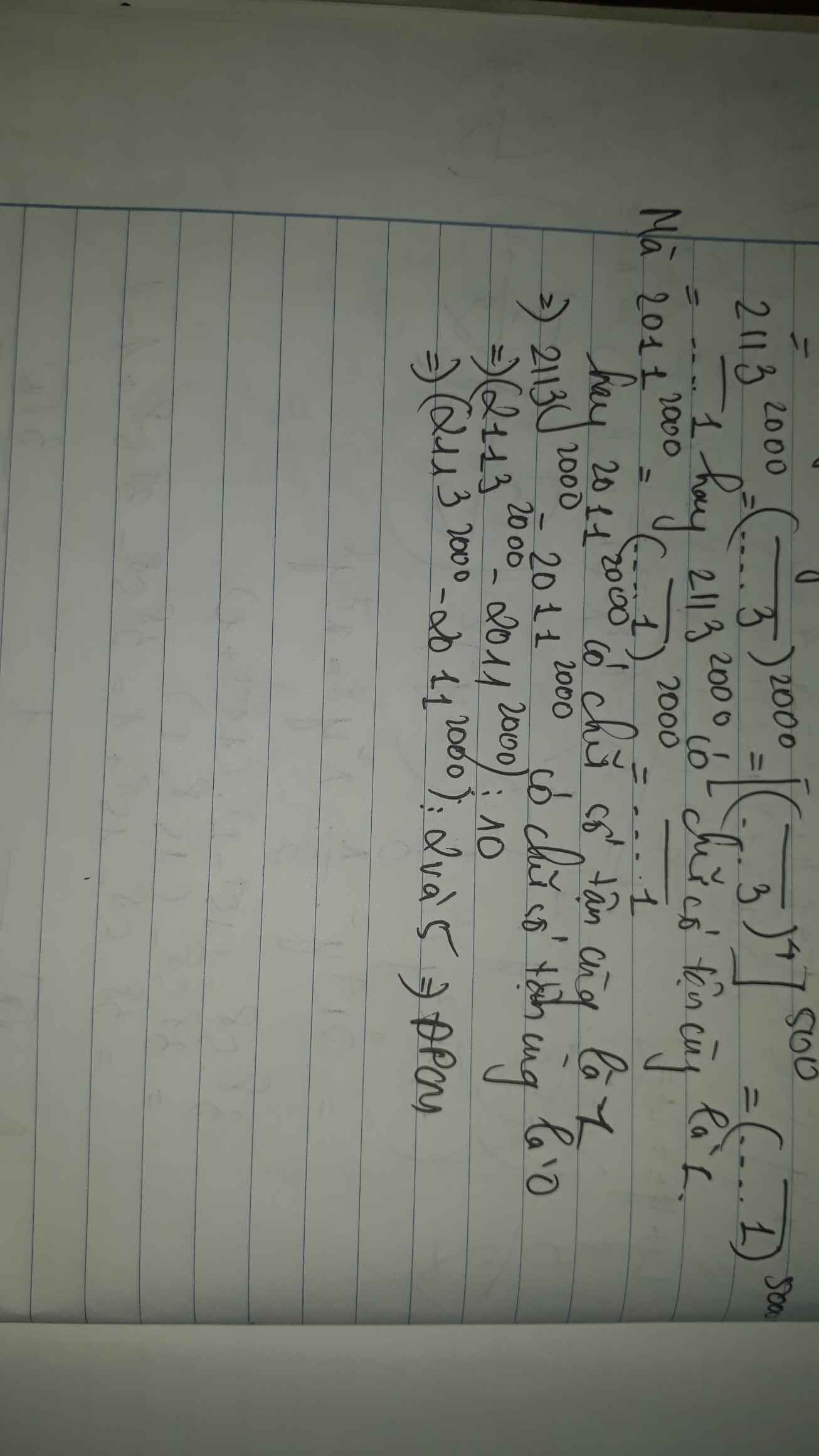
Ta có:
+) \(2113^{2000}=\left(2113^4\right)^{500}=\left(\overline{...1}\right)^{500}\) ( Tận cùng là 1 ) \(\left(1\right)\)
+)\(2011^{2000}=2011.2011...2011=\overline{...1}\) ( Tận cùng là 1 ) \(\left(2\right)\)
Từ \(\left(1\right)\&\left(2\right)\)
\(\Rightarrow2113^{2000}-2011^{2000}\\ =\overline{...1}-\overline{...1}\\ =\overline{...0}⋮2\&5\left(đcpcm\right)\)