Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: ABIO nội tiếp
ΔOEF cân tại O
mà OI là trung tuyến
nên OI vuông góc FE
góc OIA=góc OBA=90 độ
=>OIBA nội tiếp

DI//CF
=>góc EID=góc EFC=góc EBD
=>EBID nội tiếp
=>góc EDB=góc EIB
mà góc EIB=góc KOB
nên góc EDB=góc KOB
=>góc KDB=góc KOB
=>KBOD nộitiếp

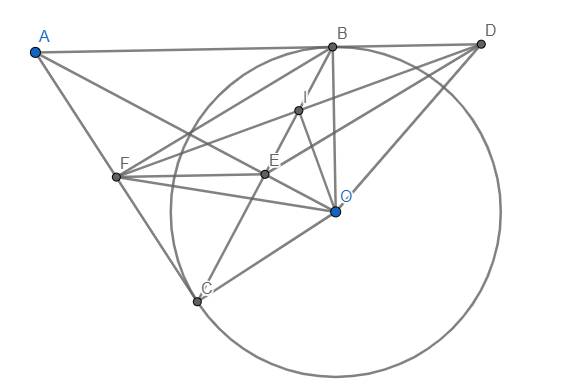
a) Nhận thấy \(\widehat{OBA}=\widehat{OCA}=90^o\) nên tứ giác ABOC nội tiếp đường tròn đường kính OA.
b) Nhân thấy \(\widehat{OID}=\widehat{OBD}=90^o\) nên tứ giác OIBD nội tiếp đường tròn đường kính OD \(\Rightarrow\widehat{IDO}=\widehat{IBO}\)
Lại có \(\widehat{IBO}=\widehat{CBO}=\widehat{BCO}\) nên dễ dàng suy ra đpcm.
c) Dễ chứng minh tứ giác OCFI nội tiếp \(\Rightarrow\widehat{OCB}=\widehat{OCI}=\widehat{OFI}=\widehat{OFD}\)
Theo câu b, ta có \(\widehat{FDO}=\widehat{IDO}=\widehat{BCO}\) nên dẫn đến \(\widehat{OFD}=\widehat{FDO}\). Do đó tam giác ODF cân tại O. (đpcm)
d) Tam giác ODF cân tại F có đường cao OI nên I là trung điểm DF.
Mặt khác, có I là trung điểm BE nên tứ giác BDEF là hình bình hành.
\(\Rightarrow\) EF//BD hay EF//AB.
Lại có E là trung điểm BC nên F là trung điểm AC (đpcm)

a: góc OBA+góc OCA=90+90=180 độ
=>OBAC nội tiếp
b: Xét ΔACE và ΔAFC có
góc ACE=góc AFC
góc CAE chung
=>ΔACE đồng dạng với ΔAFC
=>AC/AF=AE/AC
=>AC^2=AF*AE

a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)