Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Có 300 số tự nhiên nhỏ hơn 300 nên n( Ω ) = 300.
Số các số tự nhiên nhỏ hơn 300 mà chia hết cho 3 là: (297-0):3 + 1 = 100.
Số các số tự nhiên nhỏ hơn 300 mà không chia hết cho 3 là: 300 - 100 = 200 nên n(A) = 200.
Vậy 
Có 900 số tự nhiên có 3 chữ số \( \Rightarrow n\left( \Omega \right) = 900\)
Gọi \({A_1}\) là biến cố: “Số được chọn chia hết cho 2”, \({A_2}\) là biến cố “Số được chọn chia hết cho 7”.
Vậy \({A_1}{A_2}\) là biến cố “Số được chọn chia hết cho 14”, \(A = {A_1} \cup {A_2}\) là biến cố “Số được chọn chia hết cho 2 hoặc 7”.
Có 450 số có 3 chữ số chia hết cho 2 \( \Rightarrow n\left( {{A_1}} \right) = 450 \Rightarrow P\left( {{A_1}} \right) = \frac{{n\left( {{A_1}} \right)}}{{n\left( \Xi \right)}} = \frac{{450}}{{900}} = \frac{1}{2}\)
Có 128 số có 3 chữ số chia hết cho 7 \( \Rightarrow n\left( {{A_2}} \right) = 128 \Rightarrow P\left( {{A_2}} \right) = \frac{{n\left( {{A_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{128}}{{900}} = \frac{{32}}{{225}}\)
Có 64 số có 3 chữ số chia hết cho 14
\( \Rightarrow n\left( {{A_1}{A_2}} \right) = 64 \Rightarrow P\left( {{A_1}{A_2}} \right) = \frac{{n\left( {{A_1}{A_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{64}}{{900}} = \frac{{16}}{{225}}\)
\( \Rightarrow P\left( A \right) = P\left( {{A_1} \cup {A_2}} \right) = P\left( {{A_1}} \right) + P\left( {{A_2}} \right) - P\left( {{A_1}{A_2}} \right) = \frac{1}{2} + \frac{{32}}{{225}} - \frac{{16}}{{225}} = \frac{{257}}{{450}}\)
Gọi \({B_1}\) là biến cố: “Số được chọn có 3 chữ số chẵn”, \({B_2}\) là biến cố “Số được chọn có 1 chữ số chẵn và 2 chữ số lẻ”.
Vậy \(B = {B_1} \cup {B_2}\) là biến cố “Số được chọn có tổng các chữ số là số chẵn”.
Có \(4.5.5 = 100\) số có 3 chữ số chẵn \( \Rightarrow n\left( {{B_1}} \right) = 100 \Rightarrow P\left( {{B_1}} \right) = \frac{{n\left( {{B_1}} \right)}}{{n\left( \Omega \right)}} = \frac{{100}}{{900}} = \frac{1}{9}\)
Có \(4.5.5 = 100\) số có 3 chữ số có chữ số hàng trăm chẵn, 2 chữ số còn lại lẻ.
Có \(5.5.5 = 125\) số có 3 chữ số có chữ số hàng chục chẵn, 2 chữ số còn lại lẻ.
Có \(5.5.5 = 125\) số có 3 chữ số có chữ số hàng đơn vị chẵn, 2 chữ số còn lại lẻ.
\( \Rightarrow n\left( {{B_2}} \right) = 100 + 125 + 125 = 350 \Rightarrow P\left( {{B_2}} \right) = \frac{{n\left( {{B_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{350}}{{900}} = \frac{7}{{18}}\)
Vì \({B_1}\) và \({B_2}\) là hai biến cố xung khắc nên ta có:
\(P\left( B \right) = P\left( {{B_1} \cup {B_2}} \right) = P\left( {{B_1}} \right) + P\left( {{B_2}} \right) = \frac{1}{9} + \frac{7}{{18}} = \frac{1}{2}\)
a)
Biến cố AB: Số ghi trên thẻ được chọn chia hết cho cả 2 và 3.
b) Hai biến cố A và B không độc lập.
Điều này xảy ra vì nếu một số chia hết cho 2 thì nó có thể chia hết cho 3 (ví dụ: số 6), và ngược lại, nếu một số chia hết cho 3 thì nó cũng có thể chia hết cho 2 (ví dụ: số 6). => Do đó, kết quả của biến cố A ảnh hưởng đến biến cố B và ngược lại, không đảm bảo tính độc lập giữa hai biến cố này.
$HaNa$
Gọi a b c d ¯ là số có bốn chữ số đôi một khác nhau và thỏa yêu cầu bài toán.
*TH1: nếu d = 5
Có 8 cách chọn a (a khác 0 và a khác d).
Với mỗi cách chọn a có, A 8 2 cách chọn b c ¯
Có 8 . A 8 2 = 448 (số thỏa mãn).
*TH2: Nếu d= 0, có A 9 3 = 504 cách chọn a b c ¯
Nên có 504 số có 4 chữ số khác nhau chia hết cho 5 có chữ số hàng đơn vị là 0.
Vậy số có 4 chữ số khác nhau và chia hết cho 5 là: Ω A = 448 + 504 = 952 .
Đáp án D
Chọn B
Ta có 
Do đó 
Ta cũng có 
=> n(A) = 8
Vậy xác suất của biến cố A là P(A) = 8 21
Chọn D
*) Ta có: 
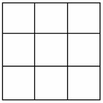
*) Tính n(A): Giả sử 8 chữ số được viết vào 8 ô trống được đánh số từ 1 đến 8
TH1: Xếp bất kỳ
Xếp hai chữ số 1, hai chữ số 2 và 4 chữ số còn lại: Có 
(cách).
TH2: Số các cách xếp sao cho không thỏa mãn yêu cầu bài toán
Xếp hai chữ số 1 đứng liền nhau: Có 
cách.
Xếp hai chữ số 2 đứng liền nhau: Có 
cách.
Số các cách xếp thuộc cả hai trường hợp trên:
+ Coi hai chữ số 1đứng liền nhau là nhóm X, hai chữ số 2 đứng liền nhau là nhóm Y
+ Xếp X, Y và 4 số còn lại có: 
(cách)
Vậy số cách xếp không thỏa mãn yêu cầu là: 
(cách)
Vậy 
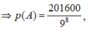
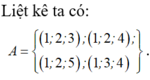
Chọn B
* Số các số tự nhiên nhỏ hơn 300 là 300 số. Lấy ngẫu nhiên một số tự nhiên nhỏ hơn 300 có suy ra n( Ω ) = 300
* Gọi A là biến cố “số được chọn không chia hết cho 4”, khi đó A ¯ là biến cố “số được chọn
chia hết cho 4”.
* Gọi số tự nhiên nhỏ hơn 300 và chia hết cho 4 là 4n (n ∈ ℕ )
* Ta có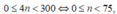
suy ra 
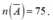Do đó 