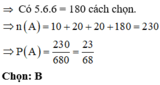Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Số phần tử của không gian mẫu: n Ω = 300
Số các số tự nhiên nhỏ hơn 300 mà chia hết cho 3 là:
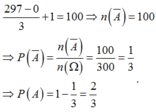
Chọn: A

Chọn đáp án A.
Số phần tử của không gian mẫu là ![]()
Tích ba số không chia hết cho 3 khi và chỉ khi cả ba số đó đều không chia hết cho 3. Các thẻ được viết số không chia hết cho 3 bao gồm 7 thẻ mang số 1; 2; 4; 5; 7; 8; 10. Số cách lấy được 3 thẻ mà tích ba số viết trên ba thẻ không chia hết cho 3 là C 7 3 = 35
Suy ra, số cách lấy được 3 thẻ mà tích ba số viết trên ba thẻ chia hết cho 3 là ![]()
![]()

Đáp án A.
Các số tự nhiên chia hết cho 7 có 5 chữ số và chữ số hàng đơn vị bằng 1 là 10031, 10101, 10171,…, 99911, 99981. Chúng lập thành một cấp số cộng có số hạng đầu u 1 = 10031 , số hạng cuối là u n = 99981 và cộng sai d = 70 .
Vậy có tất cả n số với n = u n - u 1 70 + 1 = 99981 - 10031 70 + 1 = 1286 .

Phương pháp:
Công thức tính xác suất của biên cố A là: P A = n A n Ω

Gọi A là biến cố: “Chọn ngẫu nhiên 3 phần tử của tập S sao cho tổng của 3 phần tử chia hết cho 3”.
Trong tập hợp S có 5 số chia hết cho 3 là


TH4: Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2