
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow x=2-\sqrt{3}\)
Dễ thấy x là nghiệm của PT \(x^2-4x+1\)
\(H=\left(x^5-4x^4+x^3\right)+\left(x^4-4x^3+x^2\right)+\left(5x^2-20x+5\right)+2019\\ H=\left(x^2-4x+1\right)\left(x^3+x^2+5\right)+2019\\ H=2019\)

Sửa: \(M=\frac{6}{20x^6-\left(8-40y\right)x^2+25y^2-5}\)
Đặt \(N=20x^6-\left(8-40y\right)x^2+25y^2+5\)
\(=20\left[x^6-2x^3\frac{1-5y}{5}+\left(\frac{1-5y}{5}\right)^2\right]+25y^2-20\left(\frac{1-5y}{5}\right)^2=5\)
\(=20\left(x^3-\frac{1-5y}{5}\right)^2+25y^2-\frac{4}{5}+8y-20y^2+5=20\left(x^3-\frac{1-5y}{2}\right)^2+5\left(y+\frac{4}{5}\right)^2+1\ge1\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}y=\frac{-4}{5}\\x=1\end{cases}\Rightarrow M=\frac{6}{N}\le\frac{6}{1}=6}\)
Vậy Max M=6 đạt được khi x=1; y=-4/5

21. Phân tích A thành \(A=\left(a-b\right)\left(a-c\right)\left(b-c\right)\left(a^2+b^2+c^2+ab+bc+ac\right)\). Từ đó dễ dàng chứng minh.
23. \(9y\left(y-x\right)=4x^2\Leftrightarrow9y^2-9xy=4x^2\Leftrightarrow4x^2+9xy-9y^2=0\)
Chia cả hai vế của đẳng thức trên với \(y^2>0\)được :
\(4\left(\frac{x}{y}\right)^2+\frac{9x}{y}-9=0\). Đặt \(t=\frac{x}{y},t>0\)(Vì x,y dương)
\(\Rightarrow4^2+9t-9=0\Leftrightarrow\orbr{\begin{cases}t=\frac{3}{4}\left(\text{nhận}\right)\\t=-3\left(\text{loại}\right)\end{cases}}\)
Vậy \(\frac{x}{y}=\frac{3}{4}\Rightarrow y=\frac{4x}{3}\)thay vào biểu thức được :
\(\frac{x-y}{x+y}=\frac{x-\left(\frac{4x}{3}\right)}{x+\left(\frac{4x}{3}\right)}=-\frac{1}{7}\)

Ta có: \(x=2-\sqrt{3}\)\(\Rightarrow2-x=\sqrt{3}\)\(\Rightarrow\left(2-x\right)^2=3\)\(\Rightarrow4-4x+x^2=3\)\(\Rightarrow x^2-4x+1=0\)
Lại có: \(B=x^5-3x^4-3x^3+6x^2-20x+2018\)
\(\Rightarrow B=x^5-4x^4+x^4+x^3-4x^3+5x^2+x^2+20x+5+2013\)
\(\Rightarrow B=\left(x^5-4x^4+x^3\right)+\left(x^4-4x^3+x^2\right)+\left(5x^2-20x+5\right)+2013\)
\(\Rightarrow B=x^3\left(x^2-4x+1\right)+x^2\left(x^2-4x+1\right)+5\left(x^2-4x+1\right)+2013\)
\(\Rightarrow B=x^3\cdot0+x^2\cdot0+5\cdot0+2013=2013\)


Ta có: x2 + x2y2 - 2y = 0
\(\Rightarrow\)x2 + x2y2 + y2 - 2y + 1 - y2 - 1 = 0
\(\Rightarrow\)(x2 - 1) + (x2y2 - y2) + (y - 1)2 = 0
\(\Rightarrow\)(x2 - 1) + y2(x2 - 1) + (y - 1)2 = 0
\(\Rightarrow\)(x2 - 1)(1 + y2) + (y - 1)2 = 0
\(\Rightarrow\)(x2 - 1)(1 + y2) = -(y - 1)2 \(\le\)0 V y
\(\Rightarrow\)x2 - 1 \(\le\)0 V x ( vì 1 + y2 > 0 , V y )
\(\Rightarrow\)(x - 1)(x + 1) \(\le\)0
\(\Rightarrow\)x - 1 và x + 1 trái dấu
Do đó \(\hept{\begin{cases}x-1\ge0\\x+1\le0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x\ge1\\x\le-1\end{cases}}\) ( vô lý )
Hoặc \(\hept{\begin{cases}x-1\le0\\x+1\ge0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x\le1\\x\ge-1\end{cases}}\) \(\Leftrightarrow\)-1\(\le\)x \(\le\)1 (*)
Lại có: x3 + 2y2 - 4y + 3 = 0
\(\Rightarrow\)(x3 + 1) + 2(y2 - 2y + 1) = 0
\(\Rightarrow\)(x3 + 1) + 2(y - 1)2 = 0
\(\Rightarrow\)x3 + 1 = -2(y - 1)2 \(\le\)0, V y
\(\Rightarrow\)x3 + 1 \(\le\)0, V x
\(\Rightarrow\)(x + 1)(x2 - x + 1) \(\le\)0
\(\Rightarrow\)x + 1 \(\le\)0 ( vì x2 - x + 1 = (x - 1/2 )2 + 3/4 > 0, V x )
\(\Rightarrow\)x \(\le\)-1 (**)
Từ (*) và (**) suy ra x = -1 \(\Rightarrow\)(-1)2 + (-1)2 . y2 - 2y = 0
\(\Rightarrow\)1 + y2 - 2y = 0
\(\Rightarrow\)( y - 1 )2 = 0 \(\Rightarrow\)y = 1
\(\Rightarrow\)x2 + y2 = (-1)2 + 12 = 2
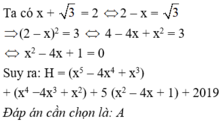
\(x^2+y^2-20x-2y+101=0\)
\(\Leftrightarrow\left(x-10\right)^2+\left(y-1\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}x=10\\y=1\end{cases}}\)
Thế vô là ra