CL
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DD
Đoàn Đức Hà
Giáo viên
13 tháng 8 2021
\(3x^2-5x-2=0\)
\(\Leftrightarrow3x^2-6x+x-2=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{3}\\x=2\end{cases}}\)
\(A=x_1+x_2=\frac{1}{3}+2=\frac{7}{3}\).
CL
cho x1, x2, x3 là 3 nghiệm của phương trình x^3-19x-30=0. Giá trị của Bt B= x1^2 + x2^2 + x3^2 là...
2
12 tháng 8 2021
x3 - 19x - 30 = 0
<=> x3 - 5x2 + 5x2 - 25x + 6x - 30 = 0
<=> x2( x - 5 ) + 5x( x - 5 ) + 6( x - 5 ) = 0
<=> ( x - 5 )( x2 + 5x + 6 ) = 0
<=> ( x - 5 )( x2 + 3x + 2x + 6 ) = 0
<=> ( x - 5 )[ x( x + 3 ) + 2( x + 3 ) ] = 0
<=> ( x - 5 )( x + 3 )( x + 2 ) = 0
đến đây dễ rồi :)
AD
12 tháng 8 2021
\(x^3-19x-30=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x-5=0\\x+2=0\\x+3=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=5\\x=-2\\x=-3\end{cases}}}\)
Vậy B=x12+x22+x32
B=52+(-2)2+(-3)2
B=25+4+9
B=38
#H
DD
Đoàn Đức Hà
Giáo viên
8 tháng 8 2021
Ta có hằng đẳng thức:
\(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
Ta thấy \(\left(x-1\right)+\left(x-2\right)+\left(3-2x\right)=0\)
do đó \(\left(x-1\right)^3+\left(x-2\right)^3+\left(3-2x\right)^3=3\left(x-1\right)\left(x-2\right)\left(3-2x\right)\)
suy ra \(\left(x-1\right)\left(x-2\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x_1=1\\x_2=2\\x_3=\frac{3}{2}\end{cases}}\)
\(S=\frac{29}{4}\).
CM
12 tháng 8 2019
Ta có x(3x – 1) – 5(1 – 3x) = 0
ó x(3x – 1) + 5(3x – 1) = 0 ó (3x – 1)(x + 5) = 0
ó x + 5 = 0 3 x - 1 = 0 ó x = - 5 3 x = 1 ó x = - 5 x = 1 3
Suy ra
x 1 = 1 3 ; x 2 = - 5 ⇒ 3 x 1 - x 2 = 3 . 1 3 - - 5 = 6
Đáp án cần chọn là: C
CM
22 tháng 12 2019
Ta có
x 2 + 3 x – 18 = 0 ⇔ x 2 + 6 x – 3 x – 18 = 0 ⇔ ( x 2 – 3 x ) + ( 6 x – 18 ) = 0
ó x(x – 3) + 6(x – 3) = 0
ó (x + 6)(x – 3) = 0
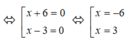
Suy ra x 1 = 3 ; x 2 = - 6 ( d o x 1 > x 2 )
=> x 1 x 2 = 3 - 6 = - 1 2
Đáp án cần chọn là: D
DD
Đoàn Đức Hà
Giáo viên
24 tháng 7 2021
Đa thức \(P\left(x\right)=x^3-3x+1\)có ba nghiệm phân biệt \(x_1,x_2,x_3\) có:
\(\hept{\begin{cases}x_1+x_2+x_3=0\\x_1x_2+x_2x_3+x_3x_1=-3\\x_1x_2x_3=-1\end{cases}}\)
\(E=Q\left(x_1\right)Q\left(x_2\right)Q\left(x_3\right)=\left(x_1^2-1\right)\left(x_2^2-1\right)\left(x_3^2-1\right)\)
\(=\left(x_1x_2x_3\right)^2-\left(x_1^2x_2^2+x_2^2x_3^2+x_3^2x_1^2\right)+\left(x_1^2+x_2^2+x_3^2\right)-1\)
\(=\left(x_1x_2x_3\right)^2-\left[\left(x_1x_2+x_2x_3+x_3x_1\right)^2-2x_1x_2x_3\left(x_1+x_2+x_3\right)\right]+\left[\left(x_1+x_2+x_3\right)^2-2\left(x_1x_2+x_2x_3+x_3x_1\right)\right]-1\)
\(=\left(-1\right)^2-3^2+2.3-1=-3\)
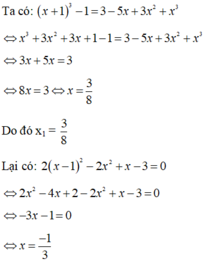
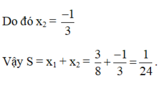
3x^2 - 5x - 2 = 0
(a = 3; b = -5; c = -2)
ta có x1, x2 là nghiệm của pt nên : x1 + x2 = -b/a = -(-5)/3 = 5/3
vậy_
Áp dụng hệ thức Vi - ét ta có : x1 + x2 = \(-\frac{b}{a}=-\frac{-5}{3}=\frac{5}{3}\)
Hoặc chưa học ở lớp 8 thì \(3x^2-5x-2=3x^2-6x+x-2=3x\left(x-2\right)+\left(x-2\right)\)
\(=\left(3x+1\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x1=-\frac{1}{3}\\x2=2\end{cases}}\Leftrightarrow x1+x2=-\frac{1}{3}+2=\frac{5}{3}\)