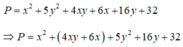
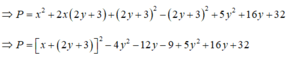
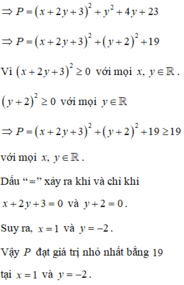
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
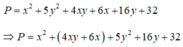
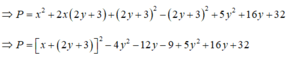
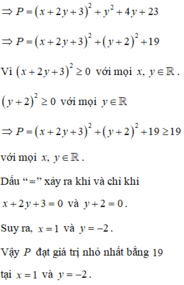
Có P = x2 + 5y2 + 4xy + 6x + 16y + 32
= [(x2 + 4xy + 4y2) + 6x + 12y + 9] + (y2 + 4y + 22) + 19
= [(x + 2y)2 + 2(x + 2y).3 + 32 ] + (y + 2)2 + 19
= (x + 2y + 3)2 + (y + 2)2 + 19
Thấy (x + 2y + 3)2 ≥ 0 với mọi x; y
(y + 2)2 ≥ 0 với mọi y
=> (x + 2y + 3)2 + (y + 2)2 ≥ 0 với mọi x; y
=> (x + 2y + 3)2 + (y + 2)2 + 19 ≥ 19 với mọi x; y
=> P ≥ 19 với mọi x; y
Dấu "=" xảy ra khi x + 2y + 3 = 0 và y + 2 = 0
Bn tự giải tiếp nha, mk ko biết có nhầm chỗ nào ko nhưng cách lm như vậy đó
Lời giải:
$A=(x^2+4y^2+4xy)+y^2+6x+16y+32$
$=(x+2y)^2+6(x+2y)+(y^2+4y)+32$
$=(x+2y)^2+6(x+2y)+9+(y^2+4y+4)+19$
$=(x+2y+3)^2+(y+2)^2+19\geq 0+0+19=19$
Vậy $A_{\min}=19$. Giá trị này đạt tại $x+2y+3=y+2=0$
$\Leftrightarrow y=-2; x=1$
Giúp em với
Bài 6
Ạ)Cho a2 +4b2+9c2=2ab+6bc+3ca. Tính giá trị của biểu thức
A=(a-2b+1)2022+(2b-3c-1)2023+(3c-a+1)2024
B) cho x,y thỏa mãn x2+2xy+6x+6y+2y2+8=0 tìm giá trị lớn nhất và nhỏ nhất của biểu thức A= x+y+2024
Ta có : (x+y)2+7x+7y+y2+6=0
( x2 + y2 + \(\frac{49}{4}\)+ 7x + 7y + 2xy ) + y2 - \(\frac{25}{4}\)= 0
( x + y + \(\frac{7}{2}\))2 = \(\frac{25}{4}\)- y2 \(\le\frac{25}{4}\)
\(\Rightarrow\frac{-5}{4}\le x+y+\frac{7}{2}\le\frac{5}{4}\)
\(\Rightarrow\frac{-15}{4}\le x+y+1\le\frac{-5}{4}\)
\(\Rightarrow\)......
lon so roi,
thay -5/4 thành -5/2 ; 5/4 thành 5/2
-15/4 thành -5 ; 5/2 thành 0
Ta có: \(15=x+y+xy\le x+y+\frac{\left(x+y\right)^2}{4}\Rightarrow\frac{t^2}{4}+t\ge15\)(\(t=x+y\))
\(\Leftrightarrow\left(t-6\right)\left(t+10\right)\ge0\Leftrightarrow\orbr{\begin{cases}t\ge6\\t\le-10\end{cases}}\)
\(P=x^2+y^2=\frac{1}{2}.2\left(x^2+y^2\right)\ge\frac{1}{2}\left(x+y\right)^2\ge\frac{1}{2}.6^2=18\)
Dấu \(=\)xảy ra khi \(x=y=3\).
\(\left(x+1\right)\left(y+1\right)=9\)
\(\Rightarrow xy+x+y+1=9\)
\(\Rightarrow xy+x+y=8\)
\(\Rightarrow x+y=8-xy\left(1\right)\)
\(K=x^2+y^2\)
\(\Rightarrow K=\left(x+y\right)^2-2xy=\left(8-xy\right)^2-2xy\)
\(\Rightarrow K=64-16xy+\left(xy\right)^2-2xy\)
\(\Rightarrow K=\left(xy\right)^2-18xy+64\)
\(\Rightarrow K=\left(xy\right)^2-18xy+81-17\)
\(\Rightarrow K=\left(xy-9\right)^2-17\ge-17\left(\left(xy-9\right)^2\ge0,\forall x;y\right)\)
\(\Rightarrow GTNN\left(K\right)=-17\)
