NH
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 5 2023
A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1
HH
0
26 tháng 12 2021
b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
\(x^4-x^3+6x^2-x+a=x^2\left(x^2-x+5\right)+x^2-x+a\)
Do \(x^2\left(x^2-x+5\right)\) chia hết \(x^2-x+5\)
\(\Rightarrow x^2-x+a\) chia hết \(x^2-x+5\)
\(\Rightarrow a=5\)
CM
11 tháng 3 2019
Ta có
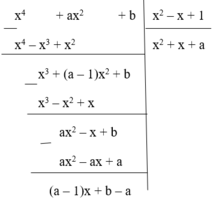
Phần dư của phép chia là R = (a – 1)x + b – A. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 1)x + b – a = 0, Ɐx
ó a - 1 = 0 b - a = 0 ó a = 1 b = 1 ó a = b
Đáp án cần chọn là: C
Z2
2
DT
0
x200 = x200 + x198 + x196 - x198 - x196 - x194 + ... + x2 = A(x)(x4 + x2 + 1) + x2
x100 = B(x)(x4 + x2 + 1) + x4
Từ đó ta có:x200 + x100 + 1 = A(x)(x4 + x2 + 1) + x2 + B(x)(x4 + x2 + 1) + x4 + 1
Từ đó ta có ta có điều phải chứng minh
tuyệt, lâu lâu mới gặp cách giải đầy trí tuệ, tôi tisk cho bn alibaba nguyễn